periodikus függvény
Tanulás a természeti jelenségek, műszaki problémák megoldásán, állunk szemben szakaszos folyamatok, amelyek lehet leírni, mint egy speciális funkciók.
A függvény y = f (x) a domain D nevezzük periodikus, ha létezik legalább egy számot T> 0, amelyben az alábbi két feltétel teljesül:
1) a pont x + T, x - T tartoznak a domain D, minden x ∈ D;
2) minden x a kapcsolatban D
f (x) = f (x + T) = f (x - T).
A szám T nevezzük időszakban f (x). Más szóval, a periodikus függvény olyan függvény, amelynek értékei ismételt egy bizonyos intervallumban. Például, a függvény az y = sin x - periodikus (1. ábra) A időszak 2π.
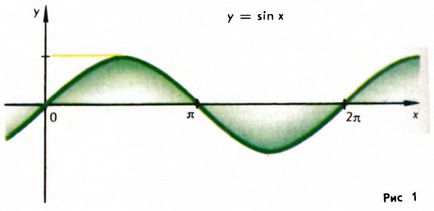
Vegye figyelembe, hogy ha a szám T az az időszak az f (x), és a szám a 2T is annak időszak 3T, és 4T és t. D. T. E. A periodikus függvény végtelen sok különböző időszakokban. Ha köztük van a legkisebb (nem nulla), akkor az összes többi időszakokban a funkciók többszöröse ezt a számot. Vegye figyelembe, hogy nem minden periodikus függvény a legkisebb pozitív időt; például az f (x) = 1 nincs ilyen időszak. Azt is fontos szem előtt tartani, hogy például az összeg két periodikus függvények, amelyeknek azonos a legkisebb pozitív időszak T0. Ez nem feltétlenül ugyanaz a pozitív periódus. Így, az összeg a függvények f (x) = sin x és g (x) = -sin x nincs legkisebb pozitív periódus, és az összeget a funkciók f (x) = sin x + sin 2x és g (x) = -sin x, legkisebb időszakok megegyeznek 2π, akkor az a legkisebb pozitív időtartamával megegyező π.
Ha az arány a két funkció között az f (x) és g (x) egy racionális szám, akkor az összeg a termék ezek a funkciók is periodikus függvények. Ha az arány a időszakok mindenütt meghatározott és az f és g jelentése irracionális szám, akkor a függvény f + g, és FG lesz már nem periodikus függvények. Például, a funkciók cos x • sin √2 • X és cosj √2 • x + sin x jelentése nem periodikus, bár a funkció sin x és cos x periódusidővel 2π, a függvény sin √2 • X és cos √2 • x időszakos korhű √2 • π.
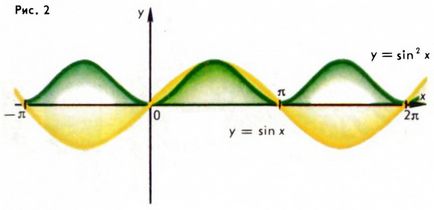
Jegyezzük meg, hogy ha f (x) - a periodikus függvény T periódus, majd az összetett függvény (kivéve persze, akkor van értelme) F (f (x)) is periodikus függvény, és a szám T fogja szolgálni az időszakban. Például, a függvény az y = sin 2 x, y = √ (cos x) (. Ábra 2,3) - periodikus függvény (itt: F1 (z) = z 2 és F2 (z) = √z). Meg kell azonban nem hiszem, hogy ha az f (x) az a legkisebb pozitív időszak T0. akkor a függvény F (f (x)) ugyanaz lesz a pozitív legkisebb időszakban; például, a függvény az y = sin 2 x a legkisebb pozitív periódus 2-szer kisebb, mint az f (x) = sin x (ábra. 2).
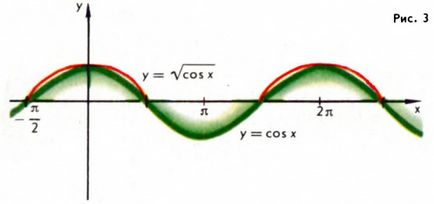
Könnyen azt mutatják, hogy ha az f függvény periódusidővel T, meghatározott és differenciálható minden pontján a valós vonal, a függvény f „(x) (származék) is egy periodikus függvény T időszakban, ugyanakkor primitív függvény F (x) (lásd. Integrál számolás) f (x) egy periodikus függvény csak akkor, ha