Ütemezése frakcionált funkció
A képlet a = k / x. ütemterv túlzás. Az 1. részben a DPA, ez a funkció nélkül kínálják elmozdulás a tengelyek mentén. Ezért csak egy paraméter k. A legnagyobb különbség a megjelenését a grafikon függ jele k.
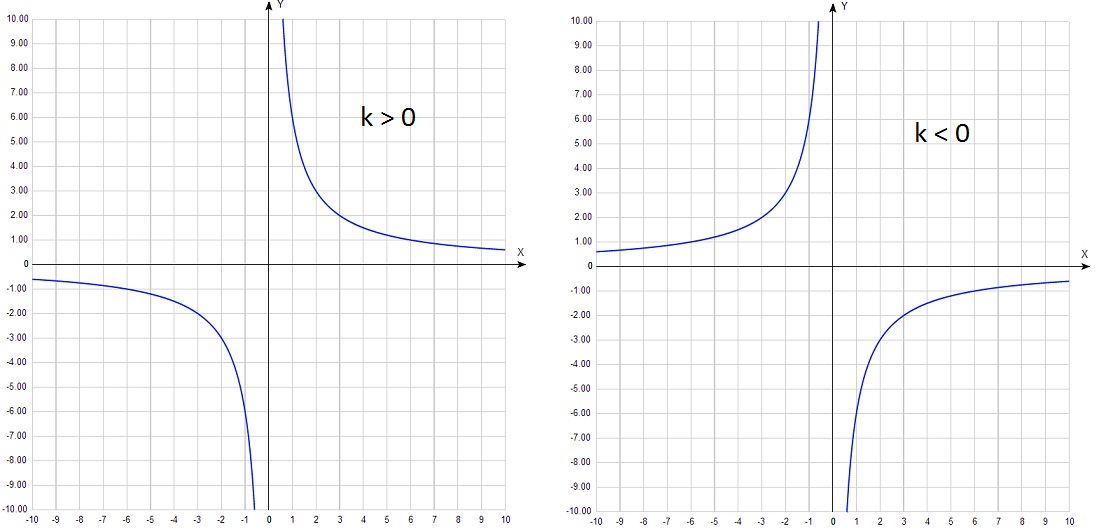
Nehezebb, hogy a különbségek a grafikonok, ha k egy jel:
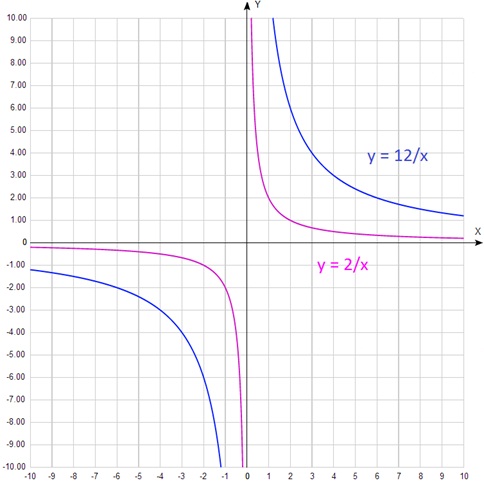
Ahogy meglátjuk, mint a nagy k. Ez fölé nyúlik hiperbola.
Az ábrán a funkciókat, amelyek a k paraméter jelentősen különbözik. Ha a különbség nem olyan nagy, hogy elég nehéz meghatározni szemmel.
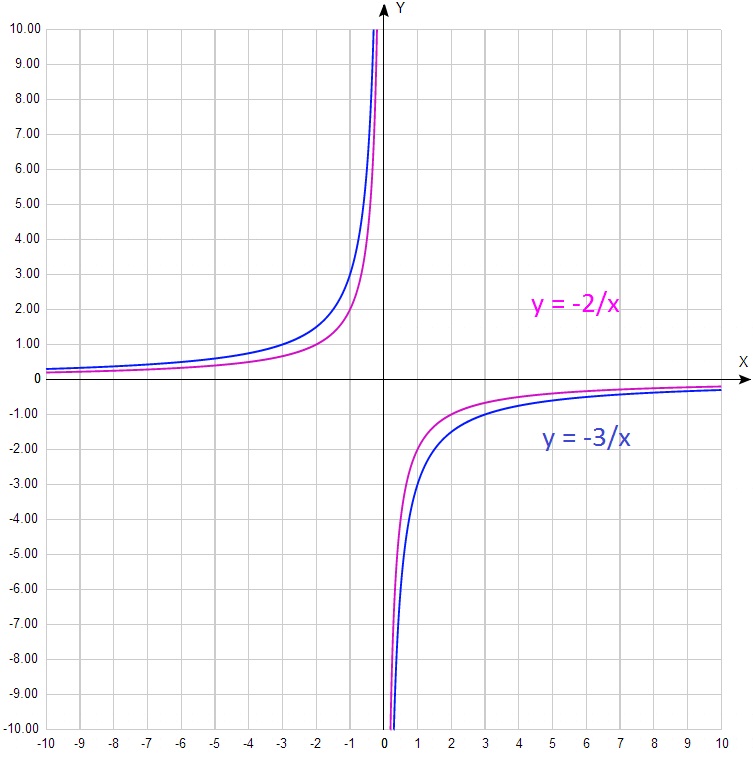
Ebben a tekintetben a „remekmű” a következő feladat, rám talált egy jó általános bemutató készül a DPA:

Nem csak, hogy a meglehetősen finom képet szorosan egymás grafika egyszerűen összeolvad. Tehát még a túlzó pozitív és negatív kizobrazheny egy koordinátarendszerben. Ez teljesen összezavarja, aki vesz egy pillantást ezt a képet. csak „hideg csillag” feltűnő.
Hála Istennek, ez csak egy képzési feladat. A tényleges megvalósítási módok, felajánlott több korrekt kiszerelésének és nyilvánvaló rajzok.
Mi lesz megérteni, hogyan határozza meg a k együtthatót az ütemezés funkció.
Általános képlet: y = k / x, ebből következik, hogy k = y · x. Vagyis, mi vehet bármely egész pont koordinátái kényelmes és szorozzuk őket - beszerezni k.
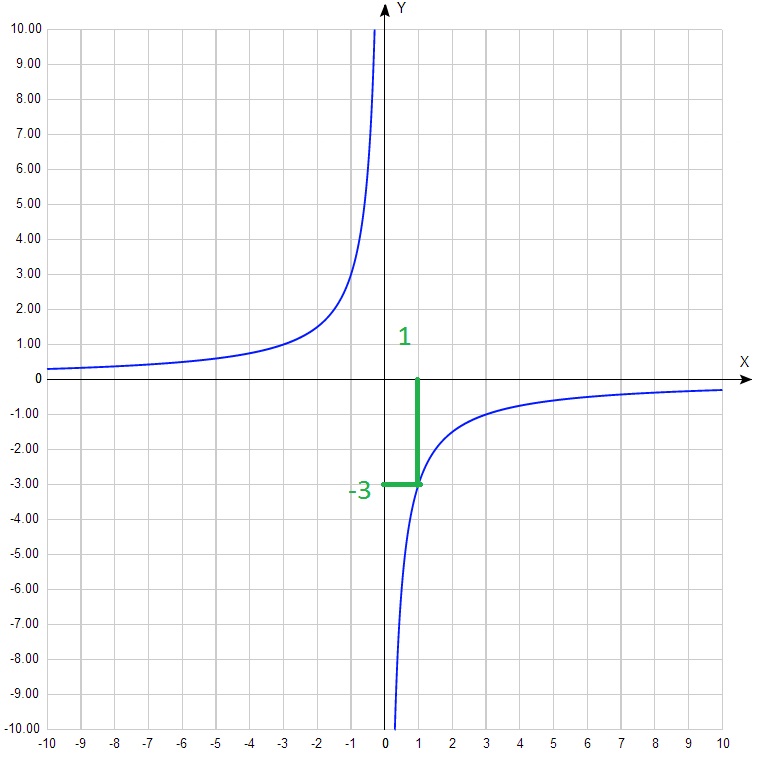
k = 1 + (- 3) = - 3.
Formula így ez a funkció: y = - 3 / X.
Érdekes, hogy fontolja meg a helyzetet egy töredék k. Ebben az esetben a képlet lehet kifejezni több szempontból is. Ez nem lehet félrevezető.
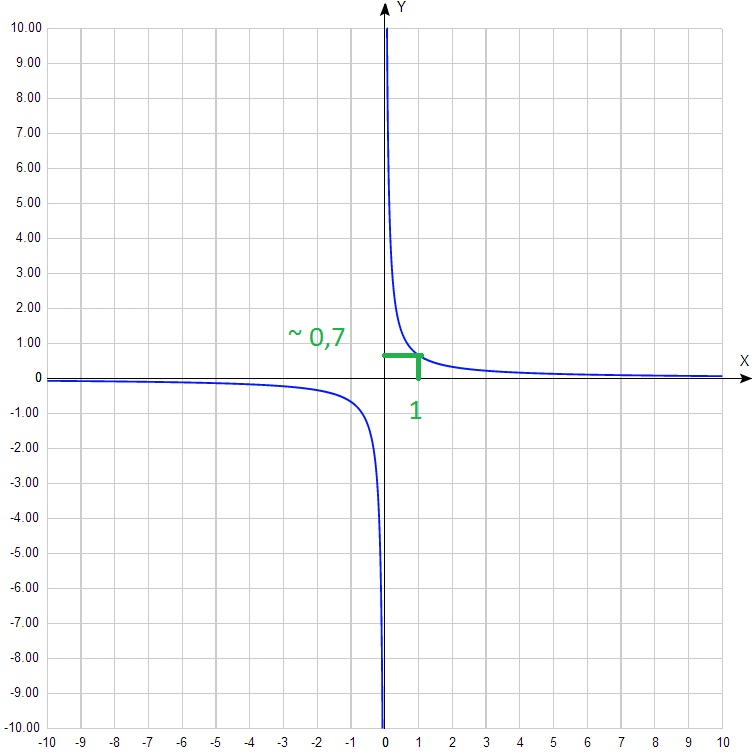
Ez a táblázat nem lehet megtalálni egy egész pontot. Ezért a k értékét lehet meghatározni nagyon kb.
k = 1 · 0,7≈0,7. Ugyanakkor azt látjuk, hogy 0 k> 0 egy hiperbola, az 1. és a 3. koordinálja szögek (negyedre) k <0 – во 2-м и 4-ом.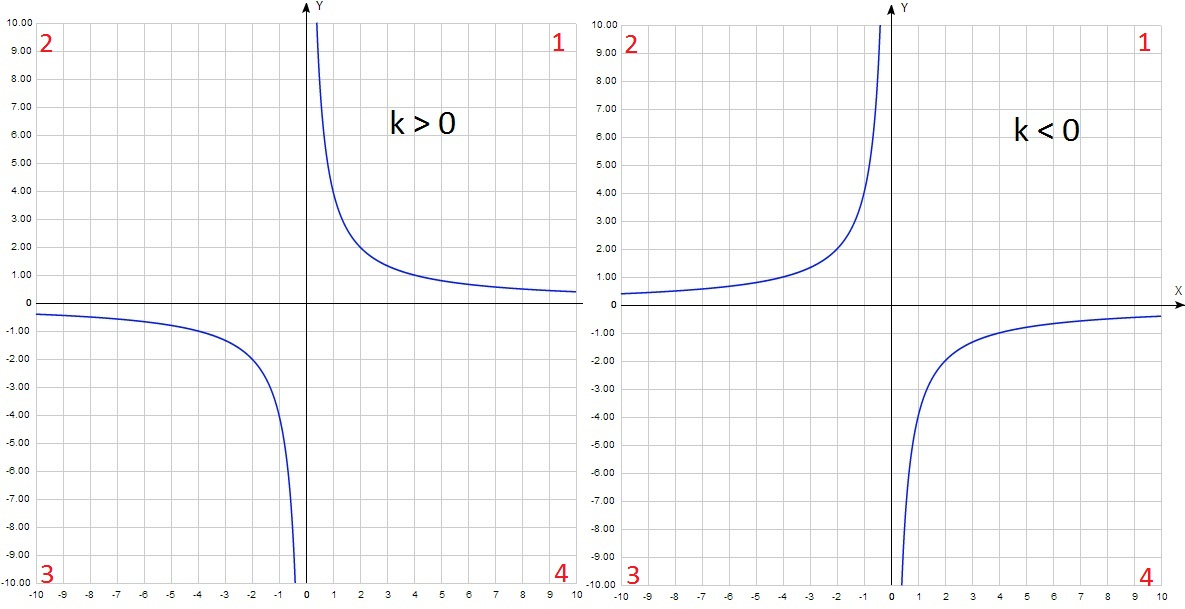
Ha k nagyobb, mint 1 modulo (K = 2 vagy k = - 2), a grafikon felett van 1 (lent - 1) az y-tengelyen, több széles.
Ha k kevesebb, mint 1 modulo (K = 1/2 vagy k = - 1/2), majd a grafikon kisebb, mint 1 (a fenti - 1) az y tengelyen, és szűkebb, „nyomott” nullára:
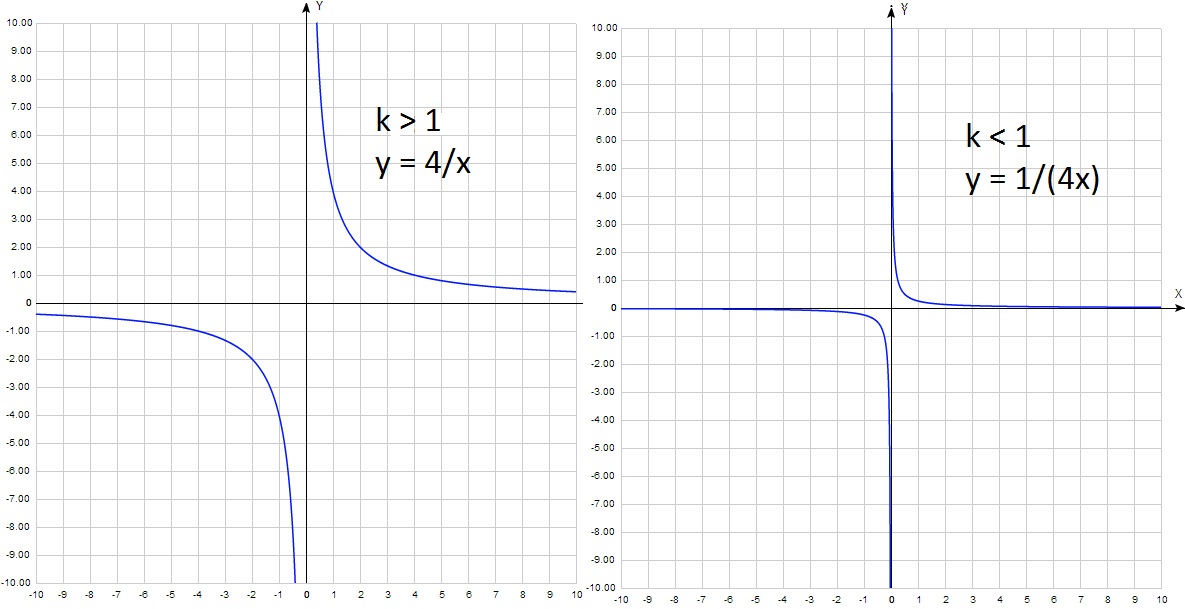
Tekintsük a probléma, javasolt az egyik kiviteli alakban a DPA:
Egyezik a grafikonok a funkciók és képletek, amelyek meghatározzák azokat.
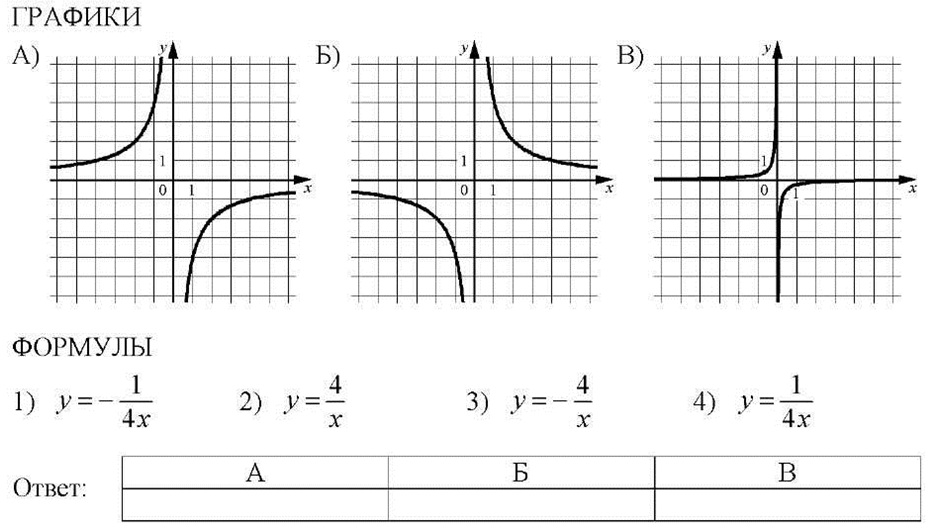
A) szerint a helyét a túlzások, a második és a negyedik sarkából a koordináta, arra lehet következtetni, hogy k <0. Этому условию отвечают формулы 1) и 3). График располагается выше у = 1, поэтому k>1 a modul, vagyis a 3)
B) álláspontja szerint a hiperbola az első és a harmadik koordináta szögek arra következtethetünk, hogy a K> 0. Ez a feltétel megfelel a képletnek, 2) és 4). Ütemezés felett van y = 1, SO, K> 1 modulo, azaz 2)
B) szerint a helyét a túlzások, a második és a negyedik sarkából a koordináta, arra lehet következtetni, hogy k <0. Этому условию отвечают формулы 1) и 3). График располагается ниже у = 1, поэтому k <1 по модулю, то есть 1)