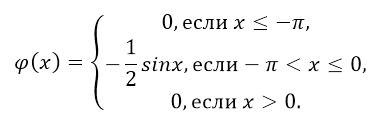Tulajdonságok valószínűségi sűrűség
Emlékezzünk a formula találni annak a valószínűsége, hogy a valószínűségi változó intervallum eléri $ (\ alpha, \ beta) $:
Nézzük mi annak a valószínűsége, hogy egy véletlenszerűen változó tartományba esik a $ (- \ infty, + \ infty $):
Nyilvánvaló, hogy egy valószínűségi változó mindig esik tartományban $ (- \ infty, + \ infty $), ezért a valószínűsége egy ilyen kapcsolat egyenlő eggyel. kapjuk:
Geometriailag, a második tulajdonság, hogy a terület a görbe vonalú trapéz által határolt grafikonja sűrűség eloszlását $ \ varphi (x) $ és az x-tengely számszerűen egyenlő eggyel.
Lehetőség van arra is, hogy megfogalmazzuk a szemközti épület:
3. tulajdonság: bármely nem negatív függvény $ f (x) \ ge 0 $ kielégíti a következő egyenletet $ \ int \ határok ^ _ = 1 $ függvénye sűrűség eloszlását egy folytonos valószínűségi változó.
A valószínűségi jelentését a sűrűség eloszlás
Adjunk a változó $ x $ növekmény $ \ háromszög x $.
A valószínűségi jelentését a sűrűség eloszlás: Annak a valószínűsége, hogy egy folytonos véletlen változó $ X $ veszi értékeket intervallumban $ (x, x + \ háromszög x) $, körülbelül egyenlő a valószínűségi sűrűség a ponton $ x $ növekmény $ \ háromszög x $:
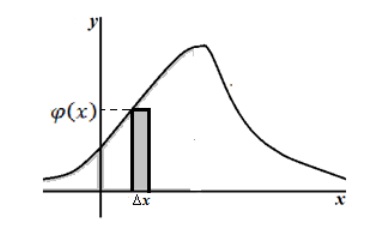
4. ábra Geometriai Vector valószínűségi értelmében folytonos véletlen változó sűrűség eloszlását.
Példák problémák megoldására a tulajdonságok használatával a sűrűség eloszlása
A valószínűségi sűrűségfüggvényének:
- Keresse együttható $ \ alpha $.
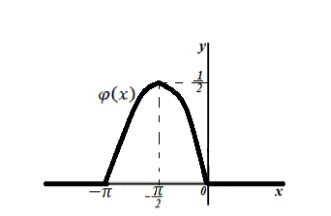
- Döntetlen a grafikont a sűrűség eloszlását.
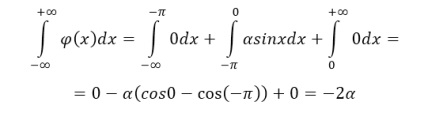
Property 2, megkapjuk:
Ez az eloszlás sűrűség függvény: