tulajdonságai funkciók
A 7. és 8. osztályok tanulmányozták bizonyos tulajdonságait funkciókat. Most gyűjtünk össze őket egy bekezdés, felidézzük a lényeg és a geometriai jelentését és egyetért, hogy milyen sorrendben felsoroljuk ezeket a tulajdonságokat, ha elolvassa a grafikon funkciót. Megjegyzés: Az összes definíciók featured számsor X, amely része a domain a funkció: az X-D (f). A gyakorlatban legtöbbször vannak esetek, amikor X - számos idő (intervallum, az intervallum, gerenda, stb.)
Funkció y = f (x) nevezzük növelésére a beállított X D (f), ha bármely két pont X1 és X2 jelentése beállítva X, úgy, hogy X1 <х2. выполняется неравенство f(х1
Funkció y = f (x) az úgynevezett csökkentésére a beállított X D (f), ha bármely monotonitási két pont X1 és X2 jelentése beállítva X, úgy, hogy X1 <х2. функции выполняется неравенство f(x1 )> f (x2).
A gyakorlatban ez sokkal kényelmesebb használni a következő szöveggel: funkció fokozott, ha egy nagyobb értéket az érvelés megegyezik egy nagyobb értéket a függvény; működése csökken, ha a nagyobb érték az érvelés megegyezik a minimális érték a funkciót.
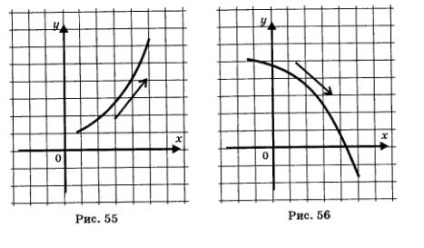
A 7. és 8. évfolyamon, azt az alábbi geometriai fogalmának értelmezése a növekvő vagy csökkenő funkciók: mozgó menetrend növekvő függvény balról jobbra, mintha mászni a dombra (ábra. 55); mozgó menetrend csökkenő függvény balról jobbra, mintha lement egy domb (ábra. 56).
Jellemzően a „növekvő függvény”, „csökkenő funkció” az általános neve egy monoton függvény, és kutatási feladatokat növelje vagy csökkentse említett tanulmány a funkciója egyhangúságot.
Megjegyzés is az egyik körülmény: ha a funkció növekszik (vagy csökken) a természetes domain, akkor általában azt mondta, hogy a funkció a növelésével (vagy csökkentésével) - anélkül, hogy a numerikus több X.
Vizsgáljuk a monotónia a funkció:
a) y = x 3 + 2; b) y = 5 - 2.
a) Vegye tetszőleges argumentumértékeket x1 és x2, és hagyja, hogy x1 <х2. Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:
Az utolsó egyenlőtlenség azt jelenti, hogy f (x1)
Funkció y - f (x) nevezzük határolja alulról egy sor X D (f), ha az összes függvény értékei a sor X nagyobb, mint egy bizonyos számú (más szóval, ha létezik olyan számot m úgy, hogy minden érték az x ∈ X kielégíti az egyenlőtlenséget F ( x)> m).
Funkció y = f (x) nevezzük egy felső korlát a beállított X D (f), ha az összes érték kisebb, mint egy bizonyos számú (más szóval, ha létezik számos N, hogy bármelyik értéke x ∈ X kielégíti az egyenlőtlenséget f (x) <М).
Ha X nincs megadva, azt feltételezzük, hogy ez egy korlátozása funkció alatt vagy fölött az egész tartományban.
Ha a funkció korlátozott, és az alsó és a felső, akkor az úgynevezett korlátozott.
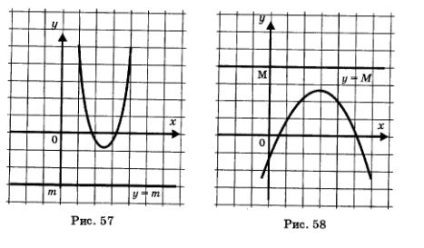
A korlátozások a funkciók könnyen olvasható rajta menetrend. ha a funkció határolt alatti grafikon terheli a fenti egy vízszintes vonal az y = m (ábra. 57); ha a funkció korlátos felett, annak grafikon terheli egy vízszintes vonal alatt y = M (llb. 58).
2. példa Teszt a korlátozott funkciójú
Határozat. Egyrészt, ez elég nyilvánvaló egyenlőtlenség (ahogyan azt a négyzetgyöke, ami azt jelenti, hogy a funkció korlátos alulról. Másrészt, van tehát
Ez azt jelenti, hogy a függvény korlátos felülről. Most nézd meg a grafikont adott funkció (ábra. 52. Az előző fejezetben). Funkciók és korlátai a tetején és alján a grafikon egész jól olvasható.
Az m szám a legkisebb érték a függvény y = f (x) az X halmazon C D (f), ahol:
1) X létezik egy pont x0. hogy f (x0) = m;
2) az összes X X kielégíti az egyenlőtlenséget m> f (x0).
Az m szám mondják legnagyobb értéke a függvény y = f (x) az X halmazon C D (f), ahol:
1) X létezik egy pont x0. hogy f (x0) = M;
2) az összes x a egyenlőtlenség X
A legkisebb függvényérték utálták a 7. és 8. évfolyamon a szimbólum, és a legnagyobb - a szimbólum.
Ha X nincs megadva, magától értetődik, hogy beszélünk megtalálni a legkisebb vagy a legnagyobb értéket a függvény az egész tartományban.
Elég nyilvánvaló az alábbi hasznos állítást:
1) Ha van egy függvénye Y, akkor korlátos alulról.
2) Ha van egy függvénye Y, akkor korlátos fölött.
3) Ha a funkció nincs alulról korlátos, akkor Y nem létezik.
4) Ha a funkció nem korlátos fenti, akkor Y nem létezik.
Keresse meg a legalacsonyabb és a legmagasabb érték a függvény
Határozat.
Ez elég világos, különösen akkor, ha igénybevétele a függvény grafikonján (ábra. 52), amely = 0 (ezt az értéket elért pontok x = -3 és x = 3), a = 3 (ezt az értéket elérte a ponton x = 0.
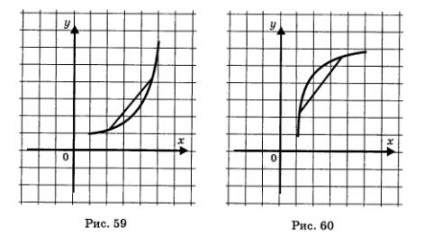
A 7. és 8. évfolyamon, már említettük két tulajdonsága funkciókat. Az első megnevezett tulajdonságait konvex függvények. Úgy tartják, hogy a függvény konvex lefelé intervallumban X, ha, csatlakoztatásával bármely két pont annak gráf (a abszcisszái X) vonalszakasz, azt találjuk, hogy a megfelelő részét a grafikon alatt fekszik által végzett a szegmens (ábra. 59). a folytonosság a függvény konvex felfelé az intervallum X, ha a funkció összekötő bármely két pont annak gráf (a abszcisszái X) vonalszakasz, azt találjuk, hogy a megfelelő részét a gráf szakasz fölé végre (ábra. 60).
A második tulajdonság - a folytonosság a funkciók X - az, hogy a függvény grafikonját az intervallum az X - szilárd, azaz Ez nem szúrások és ugrik.
Tény, hogy minden rendben van a matematika, mint mondják, „az ellenkezője”: függvény grafikonját által képviselt vonal (nélkül defekt és ugrik) csak akkor, ha igazolást folytonosság a funkciót. De a hivatalos meghatározás folyamatosságának függvényében, meglehetősen bonyolult és kényes, nem voltunk képesek. Ugyanez mondható el a konvex függvény. Megbeszélése a két tulajdonság funkciók, akkor továbbra is támaszkodni vizuális intuitív ötleteket.
Most tartsa véleményét tudásunk. Emlékezve azokat a funkciókat, hogy tanul a 7. és 8. évfolyamon, finomítani a megjelenését a grafikonok, és sorolja fel tulajdonságait funkció betartásával egy bizonyos sorrendben, például: domain; monotonitás; korlátai; . ; folytonosságát; értéktartomány; dudor.
Ezt követően, nem lesz új tulajdonságait funkciókat is változik, és a lista tulajdonságait.
1. Állandó függvény az y =
A grafikon a függvény y = G ábrán látható. 61 - párhuzamos egyenes az x tengelyre. Ez annyira érdektelen jellemzője, hogy nincs értelme felsorolni annak tulajdonságait.
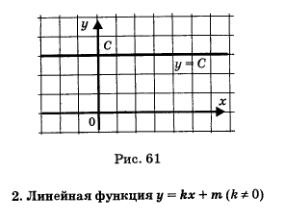
A grafikon y = kx + m jelentése egy egyenes vonal (ábra. 62, 63).
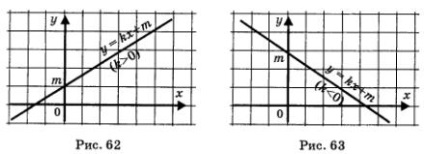
Tulajdonságok a függvény y = kx + m:
1)
2) növeli, ha k> 0 (ábra. 62), csökken, ha k <0 (рис. 63);
3) az alábbi nem korlátozódik csak az audio, audio felülről;
4) nem a legmagasabb, illetve a legalacsonyabb értéket;
5) folytonos;
6)
7) A dudor, mondván, hogy nincs értelme.
A grafikon a függvény y = kx 2 egy parabola csúcsa a eredetű, illetve az ágak felfelé irányul, ha k> (ábra. 64), és le, ha k <0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.
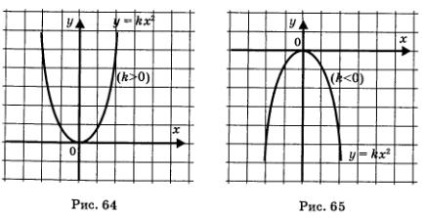
Tulajdonságai az y - k, 2:
Az eset k> 0 (64. ábra):
1) D (f) = (-∞, + ∞);
2) csökkenti a sugár (-OO, 0], fokozza az a sugár [0, + ∞);
3) korlátozott az alsó, nem korlátos a fenti;
4) = nem aktív;
5) folytonos;
6) E (f) = [0, + ∞);
7) konvex.
Megjegyzés: az intervallumban (-OO, 0] funkció csökken, és a [0, + oo) növeli. Ezek az intervallumok úgynevezett időközönként egyhangúságát függvény y = kx 2. A koncepció a monotónia a rés lehet használni más funkciókat.
Abban az esetben, hogy a <0 (рис. 65):
1) D (f) = (-∞, + 00);
2) növeli a vonal mentén (-OO, 0], csökken a sugár [0, + ∞);
3) nem alulról korlátos, korlátos a fenti;
4) nem létezik, = 0;
5) folytonos;
6) E (f)> = (-OO, 0];
7) konvex felfelé.
A grafikon a függvény y = f (x) pontja alapján; Minél több pontot az űrlap (x, f (x)) veszünk, annál pontosabb ábrázolása a diagram jutunk. Ha ezek a pontok, hogy elég sok, és az ötlet a telek alakul ki nagyobb mértékben. Ebben az esetben, az intuíció, és azt mondja, hogy a menetrend képviselővel kell egy folytonos vonal (ebben az esetben formájában parabola). És akkor olvassa a grafikon, teszünk le következtetéseket a folytonosság a funkciója, konvexitás felfelé vagy lefelé a pályán függvény értékei. Meg kell ismernünk, hogy e hét tulajdonságok „jogos” pusztán ingatlan 1) 2) 3) 4) - „törvényes” abban az értelemben, hogy képesek vagyunk, hogy alátámassza őket, utalva a pontos meghatározásokat. Másrészt tulajdonságok már csak vizuálisan intuitív ötleteket. By the way, nincs semmi baj. A matematika története ismert az emberiség hosszú ideig, és gyakran használják a különböző tulajdonságai különböző tárgyak ismerete nélkül pontos meghatározásokat. Aztán, amikor az ilyen meghatározás volt képes megfogalmazni, minden a helyére kerül.
A grafikon a függvény egy hiperbola, a tengely koordináták aszimptotái hiperbola (ábra. 66, 67).
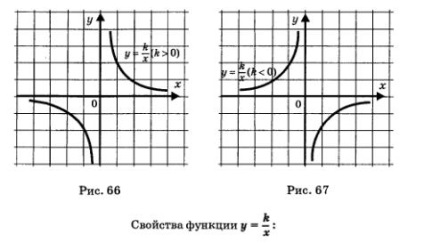
1) D (f) = (-00,0) 1U (0, + ∞);
2) ha k> 0, akkor csökken a nyitott ray (-OO, 0), és a nyitott ray (0, + ∞) (66. ábra) .; ha egy <0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) az alábbi nem korlátozódik csak az audio, audio felülről;
4) nem legkisebb vagy a legnagyobb értéket;
5) folytonos nyitott ray (-OO, 0), és a nyitott ray (0, + ∞);
6) E (f) = (-OO, 0) U (0, + ∞);
7) Ha k> 0, akkor a függvény konvex, felfelé irányuló, ha x <0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х> 0; Kültéri ray (0, + ∞) (ábra. 66). Ha egy <0, то функция выпукла вверх при х> O és domború lefelé x <О (рис. 67).
5. funkció
Grafikon egyik ága a parabola (ábra. 68). funkció tulajdonságok:
1) D (f) = [0, + ∞);
2) növeli;
3) korlátozott az alsó, nem korlátos a fenti;
4) = nem aktív;
5) folytonos;
6) E (f) = [0, + ∞);
7) konvex felfelé.
Függvény grafikonját, hogy összehozza a két gerenda:
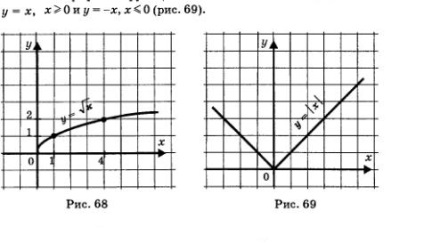
Tulajdonságok A függvény y = | x |:
1) D (f) = (-∞, + ∞);
2) csökkenti a sugár (-OO, 0], fokozza az a sugár [0, + ∞);
3) korlátozott az alsó, nem korlátos a fenti;
4) = nem aktív;
5) folytonos;
6) E (f) = [0, + ∞);
7) egy függvény feltételezheti lefelé domború.
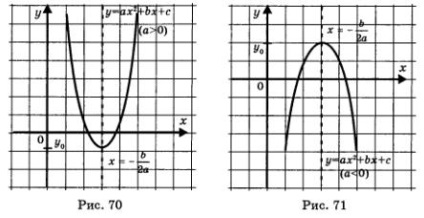
7. A függvény az y = ax 2 + bx + c
Grafikon egy parabola csúcsa a ponton
és ágak felfelé irányul, amikor a> 0 (ábra. 70), és lefelé,
ha egy <0 (рис. 71). Прямая является осью параболы.
Tekintse át ismereteket a funkciók befejezettnek tekinthető. Természetesen a következő lista nem tud a valós életben. Néhány új funkciók és tulajdonságok a velünk való találkozásra már ebben a fejezetben.
Anyagok a matematikában az interneten. kihívások és válaszok osztály, óravázlatok, jegyzetek matematika letöltés
Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.
Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.