Meghatározása korlátozott és korlátlan funkció
Legyen egy függvény az y = f (x), definiált egy sor D argumentum értékek.
A függvény y = f (x) az említett határolva D, ha létezik egy pozitív szám M, úgy, hogy minden x értékei a beállított tekinthető, az | f (x) | ≤m. Ha ez a szám M nem létezik, akkor f (x) függvény az beállítani korlátlan D.
például:
A függvény az y = sin x, meghatározott -∞
Ha az f (x) van egy határa a ponton egy, ilyenkor csak a szomszédságában egy.
bizonyíték:
Let. akkor. itt
Kapunk. Az ellenkezője nem igaz.
Test Case:
a szomszédságában 0.
- nem létezik.
Infinitezimális és azok tulajdonságait.
A függvény y = f (x) az említett infinitezimális, mint x → egy, vagy ha X → ∞, ha sem. azaz infinitezimális funkció - egy függvény, ahol a határérték ezen a ponton is nulla.
- A f (x) = (x-1) 2 elenyészően kicsi, amikor X → 1, mivel (lásd. Ábra.).
- A f (x) = TGX - infinitezimális az x → 0.
- f (x) = ln (1 + x) - infinitezimális az x → 0.
- f (x) = 1 / x- elenyészően kicsi, amikor x → ∞.
Az alapvető tulajdonságait infinitezimális funkciók (BM)
1 ° összege véges számú infinitezimális függvény olyan függvény a végtelenül kicsi.
2 ° A termék használt korlátozott funkció egy olyan funkció, infinitezimális.
3 ° A termék a két funkció függvénye az BM infinitezimális ..
4 ° A termék BM függvény egy konstans függvényt infinitezimális.
5 ° hányadosa BM funkciót egy függvény, amelynek határa nem nulla, a funkció végtelenül kicsi.
6 ° funkciót. BM inverz függvény. függvénye a végtelenül nagy. Ennek az ellenkezője igaz.
Alapvető tételek mintegy korlátokat.
1. Tétel A határérték az összeg megegyezik az összeg a határok, ha
vannak:
bizonyíték:
A kapcsolat a határeloszlástételt és végtelenül alábbiak szerint:
kap
2. Tétel Limit termék megegyezik a termék a határértékeket, ha vannak ilyenek:
bizonyíték:
A kapcsolat a határeloszlástételt és végtelenül alábbiak szerint:
Get 3. tétel A határ hányadosaként egyenlő a saját külső :. a
Feltétel: Az összes korlátozások vannak érvényben.
bizonyíték:
A kapcsolat a határeloszlástételt és végtelenül alábbiak szerint:
;
kapjuk:
4. határeloszlás megőrzi a jel az egyenlőtlenség. Ha.
bizonyíték:
ezért
következmény:
5. Tétel Ha a funkció monoton és korlátozódik (a, b), van egy határ:
20-21. Az első és második figyelemre méltó korlátok és következményei.
Teorema.Pervy figyelemreméltó limit.
Bizonyítás (geometrikus):
A következmény a tétel:
1)
2)
3)
4)
5)
Teorema.Vtoroy figyelemreméltó limit.
bizonyíték:
Binomiális tétel:
. hol.
Mi használjuk a binomiális tétel bizonyítása egyenlőtlenséget:
Arra a következtetésre jutottunk, hogy a. így van.
A következmény a tétel:
1)
2)
3)
4)
22. Az összehasonlítás végtelenül malyhvelichin (b.m.v.) Egyenértékű infinitezimális.
Let - végtelenül mennyiségek. azaz .
Definíció 1. Ha. majd - b.m.v. ugyanabban a sorrendben.
Definíció 2. Ha. majd - b.m.v. magasabb rendű.
- magasabb rendű ( "o" - olvasható a "kis").
- kisebb jelentőségű, mint a ( „O” - olvasni, mint „nagy”).
3. Ha a meghatározás. és az egyenértékű -.
Következmény 3 A definíció: a tétel. Ha ekvivalens (). és a bizonyíték:
Let - végtelenül mennyiségeket, ha azok egyenértékű).
Aztán.
BM működnek, és egyenértékűek vagy egyenértékű a BM egy rendet. ha
Képviselnek. címen.
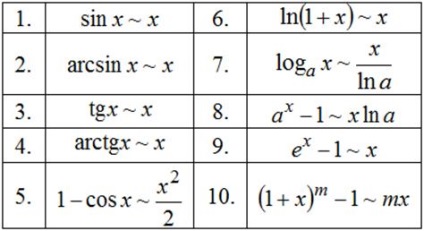
Folytonosság funkciót. Definíció a folytonosság egy pont és egy intervallum. A tétel a számtani műveletek folytonos függvények. Folyamatossága összetett funkciók. Korlátos folytonos függvények.
Függvény, amely folytonos minden pontján több régió, az úgynevezett folyamatos ezen a területen.
A funkció az úgynevezett folyamatos a jobb ezen a ponton. if.
A funkció az úgynevezett folyamatos, a bal oldalon a ponton. if.
A funkció az úgynevezett folytonos a. ha ez a folyamatos minden pontján az intervallumban.
A funkció az úgynevezett folyamatos az intervallumon. ha folytonos a. Folyamatos a jobb ezen a ponton. akkor ott folyamatos a bal pontnál. azaz.
A tétel a számtani műveleteket:
Ha az f (x) - a folyamatos t x0 .. j (x) folytonos a m. x0. akkor:
1) f (x) ± j (x) - folytonos függvény m x0 ,.
2) f × j - egy folytonos függvény m x0 ,.
3) f / j, j (x0) ¹0 - folyamatosan t x0 ..
26. Weierstrass tétel a korlátozott funkciókat egy zárt intervallum.
1) Ha a függvény folytonos az intervallumon, addig ezen a ponton a saját maximális és minimális értékek.
És a képek ábrán
az intervallum függvény folytonos, és kapta a legnagyobb érték egy ponton M. és a legkisebb m - vtochke. Ha bármilyen egyenlőtlenség :.
2) Ha a függvény folytonos az intervallumon. arra korlátozódik, hogy ezt az intervallumot, azaz van egy állandó, hogy
27. Bolzano Cauchy-tétel köztes érték függvény.
Ha folyamatos függvény a valós intervallumon vesz két értéket vesz fel és bármilyen érték közöttük.
Következmény tétellel Bolzano-Cauchy
1. A tétel a nulla folytonos függvény.
Ha a függvény folytonos egy bizonyos időközönként, és végeinél a szegmensben veszi értékek ellentétes előjelű, akkor van egy pont, ahol a függvény értéke nulla.
2. Különösen, minden páratlan fokú polinom legalább egy nulla.
28. meghatározása az inverz függvényt. A tétel a folytonosság az inverz függvény.
Definíció. Legyen a függvény az y = f (x) a domain D (f) és több R (F) értékek. Feedback F - F-1 funkció definiált függvényében domain D (f-1) = R (F), és a beállított értékek R (F-1) = D (f). oly módon, hogy az F-1 (y) = x, ha, és csak akkor, ha f (x) = y. Így, F-1 visszatér vissza y x.
példák:
Keresse inverz függvény y = 3x + 5.
Megoldás: A függvény az y = 3x + 5 van definiálva, és növeli az egész tengelyen. Ezért az inverz függvény létezik és növekszik. Egyenletet megoldva az x, kapjuk az x = (y-5) / 3.
Igazoljuk, hogy a függvény az y = kx, ahol (k ≠ 0) vissza önmagába.
Megoldás: A funkció y = kx meghatározott és monoton az egész valós tengelye, kivéve azon a ponton, x = 0. Következésképpen, van egy inverz függvényt. FIELD funkció értékek - mind valós tengelyen, kivéve a ponton y = 0. Egyenletet megoldva az x, kapjuk az x = k / y.
A tétel a folytonosság az inverz függvény:
Ha szigorúan növekvő (csökkenő) on. akkor a függvényt. amely az inverze. folytonos és szigorúan növekvő (csökkenő) on.
bizonyíték:
Tegyük fel, hogy a függvény szigorúan növekvő intervallumon.
A vizsgálat szerint a funkciók a régióban egy folytonos függvény értékeit is van különbség.
A szigorú növekvő függvény minden van egy egyedülálló pont olyan, hogy.
Következésképpen a funkció van egy inverz függvény az intervallum és a beállított értékeket.
Megmutatjuk, hogy szigorúan növekvő tovább.
Tegyük fel, hogy - a két pontot. mint például a prototípusait ezek a pontok pontok és. és.
Mert - szigorúan növekvő függvény, akkor az egyenlőtlenséget lehetséges akkor, ha azonos vagy mikor.
Tekintettel az önkényesség, arra a következtetésre jutunk, hogy a funkció - szigorúan növekvő a forgatáson.