test sebessége
Tegyük fel, hogy tudjuk, hogy a pálya egy anyagi pont. Ez azt jelenti, hogy tudjuk, a függőség r (t). Az egyszerűség kedvéért vegyük azt az esetet, amikor a mozgás pályája rejlik ugyanabban a síkban (3.1 ábra). Ebben az esetben, egy Descartes-féle koordináta-rendszer lehet megválasztani, hogy az egyik koordináta, például Z, nem változik, ez lesz nulla, a pálya ebben az esetben fog feküdni a XOY síkban.
A T1 időpontban a sugara vektor egy pont egyenlő r (t1), abban a pillanatban az idő t2 - r (t2). Során Dt = t2-t1 rádiuszvektorhoz változások Dr = r (t2) -r (t1). Ez a változás a sugara vektor az anyagi pont határozza meg elmozdulásvektorból a t idő.
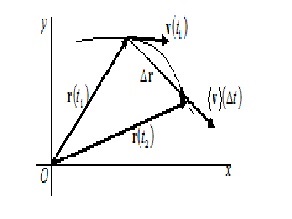
Mi határozza meg az átlagos sebesség a test a dt időintervallum alábbiak szerint:
Ha egy anyagi pont mozog egyenletesen egy egyenes vonal, az így meghatározott átlagos sebesség teljes mértékben leírják összes funkcióját egy ilyen mozgást.
Egy tetszőleges esetben, egyértelmű, hogy a v vektor semmilyen módon nem kapcsolódik a mozgáspályája szabaddá a szervezetben. Át a határt, tudjuk meg a test sebessége egy bizonyos ideig (ebben az esetben, a t1 időpontban):
Így, meghatároztuk a sebességvektor a test egy adott időpontban, mint a származék a sugár vektor adott időben a test. Három megnevezések az alkalmazott származék a szakirodalomban. Úgy látszik, hogy az így meghatározott sebességvektor egyedi módon kapcsolódik a pályáját a mozgás a test - ez irányul érintőlegesen hozzá. A test mozgása sebességvektor változhatnak, ahogy a modulus és irányát.
Egy derékszögű koordináta-rendszer:
Dr. vektor meghatározza a vektor elmozdulása során a testen dt időintervallum, az útnak a test által ez idő alatt s. Ez fogja meghatározni a görbe hossza - Lot pályáját. Csak egyenes vonalú mozgás elmozdulásvektorból modul megegyezik test mozgatandó utat, azzal a megkötéssel, hogy a vektor iránya nem változik a sebesség. Ha veszünk egy nagyon kis része egy tetszőleges pályája, akkor egy egyenes vonal, amelyen a test mozog egyenletesen egy egyenes vonal.
Modul a sebességvektor felírható:
,
óta. Ami azt mutatja, hogy az útnak a szervezet által esetben csak a sebesség vektor és az egységnyi idő alatt a mozgás:
Hagyja, hogy a nagysága a sebesség az idővel változik, ahogy a 2.2 ábrán látható.
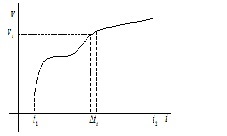
Annak meghatározására, az útnak a test által során véges dt időintervallum osszuk N időközönként D t i:
.
Path áthaladni ezen időintervallumok alatt:
.
Teljes útvonal szeli át a test, egyenlő lesz az összege:
.
Ugyanakkor, mintegy, az utat, hogy az i-edik területet lehet meghatározni:, akkor a megtett távolság közelítőleg egyenlő:
.
A pontos érték a megtett távolság szerezni átjárás a határ:
A megfelelő határértéket az úgynevezett határozott integrál.
Sikerült megállapítani a sebességet egy test egy bizonyos referenciakeret. Azt találjuk, a kapcsolat a sebesség vektorok a test (anyagi pont) meghatározott két különböző keretek K és K „(2.3 ábra). Egy bizonyos ponton az időben helyzetében a test ezekben a rendszerekben határozza meg a referencia sugara vektorok R és R”. Úgy látszik, hogy r = r0 + r”. Ha K „rendszer és a mozgó test, majd egy idő után differenciálódás kapjuk:
Ha a tetején a K „rendszer, hogy helyezze a második test, majd (2,5) lehetővé teszi számunkra, hogy meghatározzuk a sebességet az első test képest a második (relatív sebesség): v” = v-v0.
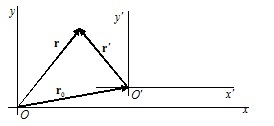
A sebességvektor az anyag pont a rendszerben, k egyenlő a sebesség vektor K „rendszer plusz a sebesség vektor K” rendszerben meghatározott K koordinátarendszerben.
Összefoglalva, mi határozza meg az átlagos sebesség a test (az átlagos értéke a sebességvektor a modul) a dt időintervallum. Ez megegyezik az útnak a szervezet osztva a mozgás:
Hasonlóképpen, ez a meghatározás az átlagos sebesség, tudjuk meg a középérték bármely fizikai mennyiség függ ideje:
Különösen, használva az általános meghatározás (2.7), hogy megtalálja az átlagos értéke a sebességvektor, mi expressziót kapjunk (2.1).