térszögbe
A szilárd szöge - a tér, amely az unió minden útja. származó egy adott pont (csúcsszög) és metsző felületi (amely az úgynevezett felületi subtending adott térszög). Különös esetekben a szilárd szög háromszögletű és poliéderes szögek. A határ a térszög egy bizonyos kúpos felület.
A térszög által mért terület aránya egy középpontú gömb a csúcsa a szög, amely be van vágva ezen a térszög, hogy egy négyzet a gömb sugarának :. $$ \ Omega \, = \, $$
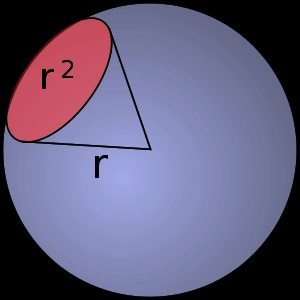
Nyilvánvaló, szilárd szögek mérjük absztrakt (mértékegység nélküli) számok. Az egység szilárd szög a SI (rendszer egység) van térszög. egyenlő a térszög vágott felülete egy egység gömb területe 1 négyzetméter egység. Teljes gömb képez térszöge 4π térszög (összes szilárd szög) a csúcsok belül található a gömb, különösen, az a gömb középpontján; így a szilárd anyag által bezárt szög bármelyik pontján a zárt felület, ez a felület teljesen fedett, de nem hozzá tartozó. Továbbá szteradiánt térszög mérhető fokokban, négyzet, négyzet és szögletes másodperc perces, valamint a frakciók a teljes térszög.
Egy kettős térszög hogy egy adott térszög meghatározott szöget Ω, álló gerendák a nyalábot alkotó bármilyen szögben Ω enyhe szögben.
Együtthatók konverziós egység térszögbe.
Kiszámítása Térszög [szerkesztés]
Egy tetszőleges felületre subtending \ (S \) térszög \ (\ Omega \), amelynek értelmében ez látható az eredete, egyenlő
ahol \ (r, \ vartheta, \ varphi \) - gömbi koordináták az elem felületének \ (dS, \) \ (\ mathbf \) - a sugár-vektor, \ (\ mathbf \) - egységnyi vektor merőleges a \ (dS . \)
A tulajdonságai a szilárd szögek [szerkesztés]
- Teljes térszög (teljes gömb) egyenlő \ (4 \ pi \) térszög.
- Összessége térszögek, két belső szilárd szögek a konvex poliéder. Ez megegyezik a teljes szög.
Az értékek bizonyos szilárd szögek [szerkesztés]
- Triangle csúcsú koordináták \ (\ mathbf_1 \), \ (\ mathbf_2 \), \ (\ mathbf_3 \) látható a származási egy térszög
\ (\ Omega = 2 \, \ mathrm \, \ frac_1 \ mathbf_2 \ mathbf_3)> _ 1 \ cdot \ mathbf_2) r_3 + (\ mathbf_2 \ cdot \ mathbf_3) r_1 + (\ mathbf_3 \ cdot \ mathbf_1) r_2>, \ )
ahol \ ((\ mathbf_1 \ mathbf_2 \ mathbf_3) \) - kevert termék adatok vektorok, \ ((\ mathbf_i \ cdot \ mathbf_j) \) - skaláris szorzata a megfelelő vektorok vastagítva jelezzük vektorok normál font - hosszuk. Ezen képlet, lehet számítani a szilárd bezárt szög tetszőleges sokszögek csúcsai ismert koordinátáit (elegendő osztani a sokszöget nem átlapoló háromszögek).
- A szilárd szög a csúcsa egy egyenes körkúp szögben α egyenlő oldatot \ (\ Omega = 2 \ pi (1 -<\href<\texttip <\cos><Косинус>>> \ frac) \). Ha az ismert bázis sugara \ (r \) és magasságát \ (H \) a kúp, a \ (\ Omega = 2 \ pi (1 - \ frac>) \). Amikor a kúp szöge kicsi, \ (\ Omega \ kb \ frac \) (\ (\ alpha \) radiánban), vagy \ (\ Omega \ kb 0,000239 \ alpha ^ 2 \) (\ (\ alpha \ ) fokokban). Így a szilárd szög, amely látható a Föld Hold és a Sun (azok szögletes átmérője megközelítőleg egyenlő 0,5 °), körülbelül 6 × 10 -5 szteradiánt vagy ≈0,0005% területe égi gömb (vagyis a teljes térszög) .
- A szilárd szög csúcsa a kocka (vagy bármely más derékszögű paralelepipedon) egyenlő a \ (\ frac \) a teljes térszög, vagy \ (\ frac \) térszög.