Szinusz, koszinusz, tangens szögek 0 ° és 180 ° - geometria - órákat 9 fokozat - Abstracts tanulságok -
Témát. Szinusz, koszinusz, tangens szögek 0 ° és 180 °
Cél: képző fogalmak szinusz, koszinusz, tangens szögek 0 ° és 180 °. Kialakulása képességek, hogy megtalálják a trigonometrikus függvények tompaszögnél.
Típusa lecke: kombinált.
Láthatóság és berendezések: táblázat „A kapcsolat a oldalai és szögei egy háromszög” [13].
a képzés színvonalának diákok szükséges megmagyarázni, mi szinusz, koszinusz, tangens szögek 0 ° és 180 °.
I. Szervezeti szakaszban
Megnyitja a tanár. Mi továbbra is tanulni geometria. A kilencedik osztály, akkor megismerkednek az új ága geometria: háromszög önkényes döntések; szabályos sokszögek; Derékszögű koordinátákat a síkban; geometriai transzformációk; vektorok egy síkban; bevezetés a szilárd geometria. Ön előtt várják az új tételek tulajdonságairól geometriai formák, érdekes feladatokat.
Kívánok leküzdeni az akadályokat, amelyek állni az utat labirintus geometria. Hagyja, hogy a tanulmány a geometria viszi az öröm szerzés nyer.
II. Önmegvalósítás támogatása ismeretek
Ahhoz, hogy ismételje meg a tájékoztatás trigonometrikus függvények akut szögek a derékszögű háromszög, akkor a táblázat előnyöket. [13]
1. Fogalmazza meghatározása szinusz, koszinusz, tangens hegyesszögű háromszög hegyesszög.
2. Keresse meg a rizst. 1 sin α, cos α, tg α, cos β, sin β, tg β.
3. A kapcsolódó sin α és cos α. ha a - hegyesszög a derékszögű háromszög?
4. Egyszerűbb a kifejezést:
a) 1 + sin 2α + cos 2α;
b) 2 cos 2a + sin 2α - 1.
5. Milyen függőség kapcsolódó sin α, cos α, α tg?
6. Keresse tg α, ahol:
a) sin α =. cos α =;
b) sin α =. cos α =.
7. Állítsa be az értéket kifejezések:
a) sin 30 °, cos 30 °, TG 30 °;
b) sin 45 °, cos 45 °, TG 45 °;
a) sin 60 °, cos 60 °, tg 60 °.
III. Fokozatos észlelés és tudatosság az új anyag
Meghatározása szinusz, koszinusz és tangens szögek 0 ° és 180 °
Tanulmány az új anyag lehet így. Készítünk egy kör közepén a származási és a sugár 1 (ábra. 2). Ez a kör az úgynevezett egység. Készítünk hegyesszög, és amely egy sugarú kör OA a pozitív irányt a Ox tengely. Legyen az A pont koordinátái (x; y). Majd derékszögű háromszög AOB, van:
Így: sine a szög α az ordináta a pont az egység kör, a sugár OA meghatározza a pozitív iránya az Ox tengely szög α. Koszinusz a szög α metszék a pont az egység kör, a sugár OA meghatározza a pozitív iránya az Ox tengely szög α. Szög tangense α az aránya az ordináta a pont a az abszcissza a ponttól, ahol a sugár OAutvoryuє pozitív iránya az Ox tengely szög α.
Megtaláljuk az értéke szinusz, koszinusz és tangens a tompaszögüek
A meghatározások, akkor meghatározza bármely szög α, 0 ° α 180 °. Ezután sin 0 ° = 0, cos 0 ° = 1, tg 0 ° = 0; sin 180 ° = 0, cos 180 ° = - l. tg 180 ° = 0.
Ha a szög α - tompa (0 ° α 90 °), az ordináta az A pont (. 3. ábra) pozitív (azaz, sin α> 0), az abszcisszán - negatív (azaz cos a 0), és az arány az ordináta és az abszcissza - negatív (azaz a tg α 0).
Következésképpen, koszinusz, tangens negatív tompaszög.
Ha α - tompaszöget (. 4. ábra), akkor cos α = OS = - OD = - cos (180 ° - α),
sin α = AC = AD = sin (180 ° - α), majd a tg α = = - = - tg (180 ° - α).
Tehát, hogy megtalálják a szinusz a tompaszög, elegendő megállapítani, hogy a szinusz a szög a szomszédos; hogy megtalálják a koszinusz, tangens a tompaszög, meg kell találni a számot, az ellenkezője a koszinusz, tangens a szomszédos sarkon.
Például, sin január 20 ° = sin (1 80 ° - 120 °) = sin 60 ° =,
1 cos 50o = - cos (1 80 ° - 150 ° C) = - cos 30 ° = -,
Tg értékénél 13 ° = - TG (1 80 ° - 135 ° C) = - tg 45 ° = - 1.
Ha osztályos tanulók nem rendelkeznek elegendő matematikai képzés, lehetséges, hogy egyszerűsítse a magyarázatot. Elég annyit mondani, hogy a szinusz tompaszögű szög egyenlő a szinusz a szög a szomszédos és a koszinusz és tangens tompaszögű szög egyenlő a számát ellenkező koszinusz és tangens a szomszédos sarokban.
Sine 0 ° jelentése 0, a szinusz 180 ° 0, a sine 90 fok értéke 1, és a koszinusza 0 ° egyenlő 1, a koszinusza -1 180 °, akkor cos A 90 fok értéke 0; Ezután tangens 0 ° és 180 ° 0, és a tangens 90 ° létezik.
IV. A konszolidáció és a megértés az új anyag
1. Számítsuk ki a szinusz, koszinusz és tangens egy szög:
a) 120 °; b) 135 °; c) 150 °.
2. Egy kalkulátor (táblázatok), keresse:
a) sin 100 °, sin 132 °, sin 175 °;
b) cos 95 °, cos 127 °, cos l 70 °;
a) tg 93 °, TG 129 °, tg 172 °.
V. Házi
1. tanulmányozása meghatározása szinusz, koszinusz, tangens szögek 0 ° és 180 °.
2. Egy kalkulátor (táblázatok), kiszámítja:
a) sin 105 °, sin 140 °, sin 165 °;
b) cos 100 °, cos 130 °, cos 160 °;
a) tg 103 °, TG 131 °, tg 163 °.
VI. Összefoglalva az eredményeket a leckét
1. Adjuk szinusz, koszinusz, tangens szögek 0 ° és 180 °.
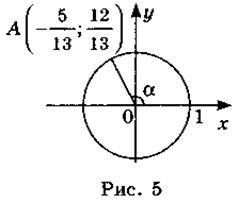
2. ábrának megfelelően. 5, talált:
a) sin α; b) cos α; a) tg α.