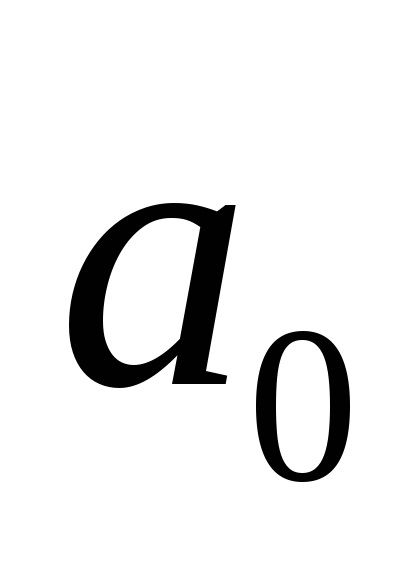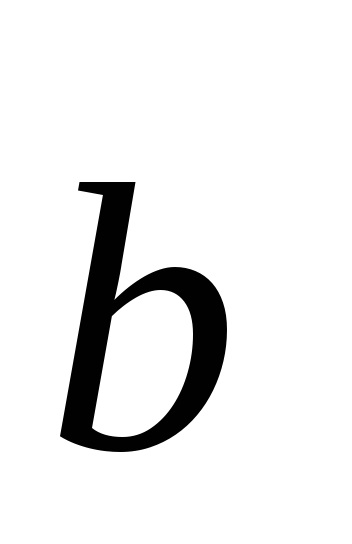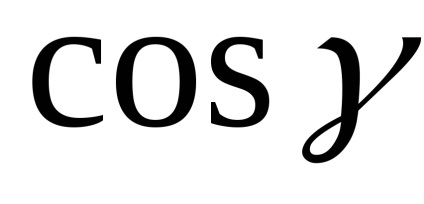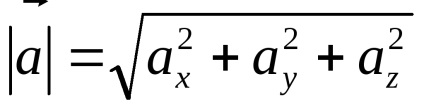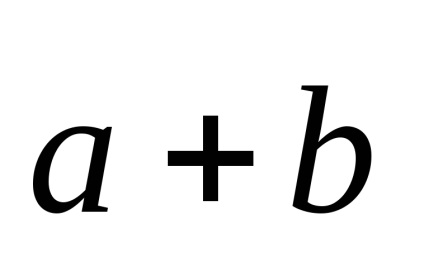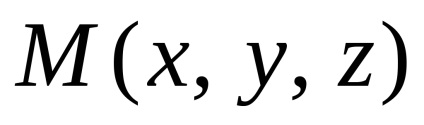Manipulálása vektorok, skalár, és a vektor termék vektorok vegyes.
háttér
I. A geometriai vektor.
Opredelenie.Vektorom (geometriai vektor) irányul vonalszakasz, azaz szegmens, amelynek egy bizonyos hosszúságú, és egy bizonyos irányba. ha
- vektor elején,
- annak végén, a vektor jelöli
vagy
. vektor
(
) Nazyvaetsyaprotivopolozhnym vektor
.
A hossza a vektor vagy modul hívják, és a szegmens hosszát jelöli
. Vektor, amelynek hossza egyenlő nulla, és a jelöli a vektor nazyvaetsyanulevym
. Vektor, amelynek hossza egyenlő eggyel, nazyvaetsyaedinichnym vektor. Az egység vektor, amelynek iránya egybeesik az irányt a vektor
, nazyvaetsyaortom ezt a vektort, és jelöljük
.
vektorok
és
nazyvayutsyakollinearnymi ha hazudnak ugyanabban a sorban vagy párhuzamos vonalak. A kollineáris vektorok jelöléssel
. Két vektor nazyvayutsyaravnymi (
) Ha vannak azonos irányban és azonos hosszúságú. Három vektor a térben nazyvayutsyakomplanarnymi. ha hazudnak ugyanabban a síkban vagy párhuzamos síkokban.
II. Műveletek vektorokkal.
A vektorhalmaz vezetünk művelet úgynevezett vektor hozzáadásával. Ez a művelet lehet meghatározni sem a paralelogramma szabály (ha a vektorok
és
, részesei paralelogramma, akkor az összegük a vektoros
, ahol
- a negyedik csúcsa a paralelogramma), vagy pravilomtreugolnika (ha a vektorok
és
az oldalán egy háromszög, akkor az összegük a vektor
).
Ez könnyen ellenőrizhető a következő tulajdonságokat a művelet a vektorhalmaz:
Ezért, tekintettel a hozzáadásával vektorhalmaz képez Abel-csoport.
terméket a vektor
száma
Ez egy vektor
, amelynek a hossza
és az irányt a vektor
, ha
; Az ellentétes irányban a vektor
, ha
. Megjegyezzük, hogy
.
A termék számának vektor a következő tulajdonságokkal rendelkezik:
A sor geometriai vektorok
A bemenet rajta műveleteket nazyvaetsyavektornym helyet.
III. vektor koordinátái.
Tekintsük a térben
A rá kiszabott egy derékszögű koordináta-rendszerben. enged
és
- Három egység vektorok áradó eredetű az irányban a derékszögű tengelyei rendre
és
. Ezek a vektorok nazyvayutsyaortami koordinátatengelyeken. Hagyja, hogy a vektor
is kezdőpont
(Eredete). Vetítjük a végén a vektor
a koordinátatengelyeken. A kapott nyúlványok felírható videi
, ahol
és
- sarkok, amely egy vektor
rendre Koordinátatengelyek
és
. szám
és
nazyvayutsyanapravlyayuschimi koszinuszok vektor
. vektor
és a nyúlványok a koordinátatengelyeken gyöke az egyenletnek
.
trojka vektorok
nazyvaetsyabazisom vektortér
. és az egyenlet fentebb leírt - vektor bomlás
alapján
. a számok
vannak nazvaniekoordinat vektor
az alaphoz képest
. Mivel a koordinátákat a vektor
tekintetében ezen az alapon a nyúlványok a vektor a koordináta-tengelyen a vektor hosszúsága és koordinátái kapcsolódnak, amelyet a képlet
.
Behelyettesítve ezen egyenlet a koordinátákat a vektor, kifejezve iránykoszinuszokat könnyű megszerezni egyenlőség
,
amely kielégíti a iránykoszinuszokat bármely vektor. Megjegyezzük, hogy a iránykoszinuszokat koordinátái az egység vektor vektor
.
Mivel a koordinátákat a vektor
teljesen meghatározza azt, akkor adja meg a kijelölés
és cserélje műveletek vektorokkal megadott műveletek koordinátákkal. Mivel vektor túlmenően
lehet helyettesíteni hozzáadásával a koordináták:, azaz,
és vektor szorzata száma
- megszorozzuk a koordinátákat ezen a számon: vagy.
egyenlőség vektorok
koordinálja a nyelvi magában foglalja az egyenlő azok eredete, és egy egyenesbe esik
- arányossága eredetük
.
Tegyük fel, hogy van két pont
és
. Ezután a vektort
felírható. Különösen, dlyaradius-pont vektor
mi van a képlet, vagy
.
Kapcsolódó cikkek