Semiregular polyhedra - studopediya
Semiregular poliéder egy természetes kiterjesztése a rendszeres poliéder. Ez konvex poliéderek, akiknek az arca szabályos sokszögek - esetleg eltérő oldalak számát, és minden csúcs azonos arcok száma. Legtöbbjük fedezték Archimedes. De nyitott és a XX században.
A legegyszerűbb az archimédeszi poliéderek kapott rendszeres poliéder „csonka” művelet, amely a elvágva a sarkokban a síkok a poliéder. Így, ha a vágott szögei a tetraéder síkok, amelyek mindegyike csökkenti egy harmadik része, az éle egy csúcsból, megkapjuk csonkolt tetraéder. amelynek nyolc oldala (1. ábra). Négyen - szabályos hatszögek és négy - egyenlő oldalú háromszög. Minden csúcsa a poliéder konvergálnak három arcot.
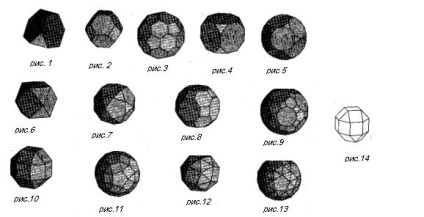
Ha az így vágott csúcsa a oktaéder és ikozaéder, akkor megkapjuk rendre egy csonka oktaéder (2. ábra), és egy csonkított ikozaéder (3. ábra). Megjegyzés. hogy a felület a futball-labda felülete készül formájában csonka ikozaéder. A kocka, és a dodekaéder is kap csonka kocka (4. ábra), valamint a csonka dodekaéder (5. ábra).
Annak érdekében, hogy egy másik szabályos poliéder, tartsa a kocka vágósík közepén keresztül az élek egyik csúcsa. Az eredmény egy semiregular poliéder, amely az úgynevezett cuboctahedron (6. ábra). Lapján hat terek, mint a kocka, és nyolc egyenlő oldalú háromszög, mint az oktaéder. Innen a neve - cuboctahedron.
Hasonlóképpen, ha a HOLD keresztül a felezőpontja élek egyik csúcsa egy dodekaéder a lehallgató síkokban, kapunk egy poliéder, amely az úgynevezett ikozidodekaéder (ábra7). Ő húsz arcok - szabályos háromszögek és tizenkét arcok - rendszeres ötszög, azaz az összes arcok a ikozaéder és a dodekaéder.
Egy másik két poliéder nevezzük cuboctahedron csonkolt (8. ábra), és egy csonkított ikozidodekaéder (9. ábra), bár nem tudnak csonkolás cuboctahedral és ikozidodekaéder. Elvágva szögek ilyen poliéder nem ad terek, és téglalapok.
Áttekintettük ből 9 13 által leírt Archimedes semiregular poliéder. A fennmaradó négy - poliéderek egy bonyolultabb típus.
A 10. ábrán látjuk rombokubooktaedr. A felület áll egy kocka, és oktaéder arcok, amelyhez hozzáadunk további 12 négyzetek.
A 11. ábra rhombicosidodecahedron amelynek felülete áll az arcok az ikozaéder és egy dodekaéder további 30 négyzetek. A 12., 13. ábrákon az úgynevezett simous (mopsz) kocka, és simous (mopsz) dodekaéder, amelyeknek felületei állnak, kocka vagy dodekaéder körül szabályos háromszögek.
Ezen kívül tizenhárom szervek Archimedes-szám félig poliéder tartalmazza 14. poliéder nevezett psevdoarhimedovym (14. ábra). Ez származik rombokubooktaedra fordult az alján a tálat 45º.
Természetesen, a meghatározó ECLI semiregular poliéder gyengíti a második feltétel, hogy lehetséges, hogy más poliéderek megfelelnek ennek a meghatározásnak. Legalább van öt polyhedra nyert forgó alkatrészeket.
Tehát, ha forgatni az alsó vagy felső csésze ikozidodekaéder 36 °, kapunk egy új poliéder, az arcok, amelyek rendszeresen ötszög és a háromszög konvergálnak, és négy borda mindegyik tetején.
Rátérve rhombicosidodecahedron tálak kaphat további négy poliéder, akiknek az arca szabályos ötszög négyzetek és háromszögek, és konvergál a négy szélét minden csúcs.
Mi az a meghatározás, a semiregular poliéder helyes? Mi az a meghatározás azt jelenti Archidamus, aki leírta a tizenhárom semiregular poliéder? Vajon tudni psevdoarhimedovom szerv vagy nem hiszem, hogy lehetséges, hogy kapcsolja be a tálba cuboctahedral? Sajnos, a meghatározás Félszabályos poliéder, amelynek felhasználásával Archimedes, nem jön le hozzánk. Úgy tűnik, Archimedes nem tartotta psevdoarhimedov poliéder Félszabályos poliéderek.
Sőt, a megjelenése psevdoarhimedov poliéder nem egy „jobb”, mint Arkhimédész poliéder. De mi határozza meg a „korrektség”?
Ábrázoljuk semiregular poliéder készülhet átlátszó anyagból, és nézd át az egyik N-szén-arc. Látni fogjuk a többi arcot, amelyet egy bizonyos sorrendben. Ugyanazt a képet látjuk, ha megnézzük egy másik n szögű arca ezt poliéder. Ez a tulajdonság birtokában az összes félig szabályos poliéder, és psevdoarhimedov poliéder - nincs. Ha megnézzük a tetején egy szögletes arcú, szögletes arc oldalán keresztül látjuk, más elrendezésben a többi arc.
Egy matematikai szempontból helyes határozza meg a jelenléte szimmetriák, azaz mozgások kezében egy poliéder önmagához.
Archimedes szervek következő tulajdonságot: bármely két csúcsot létezik egy szimmetria, amelyben az egyik csúcspontot mozog a másikra. Ez azt jelenti, hogy nem csak az összes poliéder szögeit ugyanaz, de hogy bármely két poliéder szögeit poliéder van egy mozgalom, amely elveszi az egyik a másiknak. Persze, ez egy erősebb feltétel, mint az egyenlőség poliéder szögek. Ez a feltétel nem teljesül psevdoarhimedov poliéder.
Így három lehetőség meghatározására semiregular poliéder.
1. Definíció Félszabályos poliéderek úgynevezett konvex poliéder, amelynek a felülete alkotja szabályos sokszögek - esetleg eltérő számú oldala - és minden vertex azonos számú bordák. Ebben az esetben, amellett, hogy a két végtelen sorozatát prizmák és antiprisms, van legalább 19 ilyen poliéder.
2. Definíció semiregular poliéder úgynevezett konvex poliéder, amelynek a felülete alkotja szabályos sokszögek - talán egy másik oldalainak száma - és ezek mindegyike polyhedral szögek egyenlők. Ebben az esetben, amellett, hogy a két végtelen sorozata prizmák és antiprisms, van 14 ilyen poliéder - 13 szervek és psevdoarhimedov Archimedes poliéder.
3. meghatározása semiregular poliéderek úgynevezett konvex poliéder, amelynek a felülete áll szabályos sokszögek - esetleg eltérő számú oldalról - és bármely két csúcsa van egy szimmetria a poliéder, amely átalakítja az egyik a másikba. Ebben az esetben, amellett, hogy a két végtelen sorozat, van 13 ilyen poliéder - archimédeszi poliéder.
Feltételezhetjük, hogy Arkhimédész használta a harmadik definíció. [9]