Selejtező kapcsolat feszesség korrelációs együttható, a korrelációs index, rugalmassági együtthatók és

Home | Rólunk | visszacsatolás
Együtt az építőiparban a regressziós egyenlet értékelik közelsége a kapcsolat
között jelenségek (változók között).
Connection szorítás esetében lineáris függés jellemzi
minta korrelációs együttható RXY
Szelektív korrelációs együttható RXY van társítva a lineáris regressziós koefficiens b arány
Minél közelebb van az RXY egységet, annál jobban a lineáris összefüggés, és annál jobb a lineáris összefüggés összhangban van a mért adat. Amikor RXY = 1 linket válik funkcionális, t. E. Az arányt végre az összes megfigyelések.
Amikor RXY> 0 egy közvetlen kapcsolat, a RXY <0 – обратной.
Az egyenlet lineáris regresszió, valamint egy lineáris függvény mutató kiegészített szorítás változók közti összefüggéseket. nevezetesen index korrelyatsiiR
Ennek értéke index határain belül; Az közelebb van, annál közelebb a kapcsolatot ezek a tünetek, annál megbízhatóbban talált a regressziós egyenletet.
Gazdasági tanulmányok széles körben használják olyan indikátort, például a rugalmassági tényező, különösen az átlagos rugalmassági tényező.
Az átlagos rugalmassági tényező százalékos arányát jelzi az átlagos aggregált faktor értékek x y változásokat eredményezhet az átlagos értéket, amikor a változó tényező x 1%:
A lineáris függvény:
A teljes intézkedés az általános minősége a regressziós egyenlet (a megfelelő egyenletek
Regressziós statisztikák) egy determinációs együttható R2.
Abban az esetben, gőz regressziós együttható meghatározása egybeesik a négyzet a korrelációs együttható:
Általában a meghatározás együtthatója a következő képlettel számítjuk:
Hadd magyarázzuk értelmében a determinációs együttható. Hagyja empirikus regressziós egyenlet:
Ezután a megfigyelt (tényleges) érték yi. i = 1, 2, .... n, yi modell összegtől eltérő EI:
Az utóbbi összefüggést lehet újraírni az alábbiak szerint:
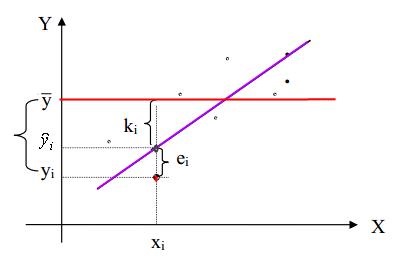
ahol - i -edik eltérés (megfigyelt) tekintve az átlagos értéke a függő változó Y;
- eltérés az i-edik pont a regressziós vonal;
- eltérés az i-edik pont a modell érték. mérve a regressziós egyenes.
Minden eltéréseket számított a függő változó tengely (lásd. Ábra. 3.3).
Emeljük egyenlet mindkét oldalát (*) a téren, és összegezzük a kapott értékeket n mintatérfogat:
Meg lehet mutatni, hogy (a bizonyítás elhagyjuk az edzéshez). Aztán ott van az alábbi összefüggést:
- összesen (teljes), a négyzetösszeg (lehet értelmezni, mint egy közös intézkedés spread (diszperzió) képest az Y változóhoz). (TSS)
- magyarázata a négyzetösszege értelmezhető intézkedés elterjedt, indokolható a regresszió. (ESS)
- maradék (megmagyarázhatatlan) négyzetösszege amely intézkedés a maradék, megmagyarázhatatlan regressziós egyenletet spread (spread pontok körül a regressziós vonal). (RSS)
Osztódó (3,13), a bal oldalon egy részét, ezt kapjuk:
Bemutatjuk a jelölést. kapjuk (3.12). Nyilvánvaló, hogy a meghatározás együtthatója R 2 határozza meg a változás a függő változó, megmagyarázható regressziós Y az X
meghatározza a scatter frakciót függő változó, megmagyarázhatatlan regressziós Y az X
A fenti megfontolásokból következik, hogy általában a kapcsolatban 0 ≤ R 2 ≤ 1.
A determinációs együttható R2 olyan intézkedés, hogy meghatározza, milyen mértékben által talált regressziós vonal adja a legjobb eredményt magyarázatára a viselkedését a függő változó Y, mint a vízszintes vonal az Y =.
Következésképpen, minél közelebb van a lineáris kapcsolat X és Y közötti, minél közelebb van a meghatározás együtthatója R 2 egységét. A gyengébb Ebben az összefüggésben az R2 közelebb a nullához.