Sajátvektorok és sajátértékek a lineáris operátor - studopediya
A vektor X ≠ 0 nevezzük sajátvektor a lineáris operátor mátrix Egy, ha van egy szám l, hogy a AX = Lx.
A szám l nevezett sajátérték (mátrix), amely megfelel a vektor X.
Más szóval, a sajátvektor - egy vektor, amely az intézkedés alapján lineáris operátor belép kollineáris vektor, vagyis egyszerűen megszorozva néhány számot. Ezzel szemben a nem megfelelő vektorok a nehezebb.
Írunk a saját meghatározása egy vektor formájában egyenletrendszert:
Transzfer az összes feltételt a bal oldali:
felírhatjuk az utolsó rendszer mátrix formában az alábbiak szerint:
Az így kapott rendszer mindig nulla oldat X = O. Az ilyen rendszerek, amelyekben az összes állandó kifejezések nulla, az úgynevezett homogén. Ha a mátrix rendszer - egy négyzet, és annak meghatározó nem nulla, akkor a Cramer szabály, mindig kap egy egyedi megoldás - nulla. Belátható, hogy a rendszer nem triviális megoldás akkor és csak akkor, ha a meghatározója ez a mátrix nulla, azaz
Ez az egyenlet ismeretlen l nevezett karakterisztikus egyenlet (karakterisztikus polinomja) A mátrix (lineáris operátor).
Belátható, hogy a karakterisztikus polinomja lineáris operátor független a választott alapon.
Például, azt látjuk, a sajátvektor és sajátérték egy lineáris operátor által meghatározott mátrix =.
Ehhez össze a karakterisztikus egyenlet | A - LE | = (1 - l) 2 - 36 = 1 - 2L + l 2 - 36 = L 2 - 2l - 35 = 0; A = 4 + 140 = 144; sajátértékek l1 = (2-12) / 2 = -5; L2 = (2 + 12) / 2 = 7.
Ahhoz, hogy megtalálja a sajátvektorok, megoldására két egyenletrendszerek
Az első ilyen kiegészített mátrix formájában
,
A második egy kiterjesztett mátrix formájában
,
A sajátérték (-5) és az összes vektorok formájában ((2/3) a C1, C1) a sajátérték-7 - (C (2/3)) Így a sajátvektorai Ezen lineáris üzemben minden vektor faj.
Belátható, hogy a mátrix a üzemeltető a alapján álló annak sajátvektorok diagonális, és alakja:
,
ahol li - sajátértékei ez a mátrix.
Ezzel szemben, ha a mátrixot néhány alap átlós, mind a vektorok ezen az alapon lesz a sajátvektorait ez a mátrix.
Az is lehetséges, hogy azt mutatják, hogy ha a lineáris üzemeltető n különböző sajátérték, a megfelelő sajátvektor lineárisan függetlenek, és a mátrix az üzemeltető a megfelelő alapon diagonális.
Mi magyarázza ezt az előző példában. Vegyünk tetszőleges nem nulla értékek, és a C1. de úgy, hogy a vektorok X (1) és X (2) lineárisan függetlenek, azaz a alapját képezték. Tegyük fel például, hogy a c = c1 = 3, akkor a X (1) = (-2, 3), X (2) = (2, 3). Nézzük ellenőrizze a lineáris függetlenség vektorok:
= -12 ≠ 0. Ebben az új alapján mátrix formában van A * =.
Ennek ellenőrzéséhez használjuk a képlet A = C -1 * AS. Először is, azt látjuk, C-1.
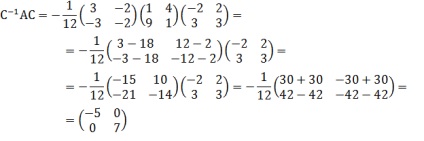
Kvadratikus alak f (.. X1 X2 xn) n változók nevezik az összeg minden egyes tagja, amely egy négyzet a változók közül az egyik, vagy a termék a két különböző változót, együtt bizonyos hányados: f (.. X1 X2 xn) = (aij = Aji ).
A mátrixot az együtthatók, az úgynevezett mátrix négyzetes formában. Ez mindig egy szimmetrikus mátrix (azaz mátrix, szimmetrikus a fő diagonális, aij = Aji).
A mátrix jelöléssel, a kvadratikus alak f (X) = X T AX, ahol
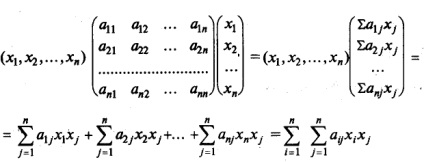
Például egy kvadratikus alak, írunk mátrix formában.
Ehhez találunk a mátrix a kvadratikus alak. A diagonális elemei megegyeznek a négyzetek az együtthatók a változók, és egyéb elemek - Fél a megfelelő együtthatók a kvadratikus alak. ezért
Legyen oszlop mátrix X változó kapott nem degenerált lineáris transzformációs mátrix oszlop-Y, azaz X = CY, ahol C - nonsingular n-ed rendű. Ezután a kvadratikus alak
f (X) = X T AX = (CY) T A (CY) = (Y T C T) A (CY) = Y T (C T AC) Y.
Ily módon, amikor a nem-degenerált lineáris transzformáció a mátrix a kvadratikus forma formájában: A * = C T AC.
Például, találunk egy kvadratikus alak f (y1 y2.), Nyert a kvadratikus formájában f (x1, x2). = 2x1 2 4x1 + x2 - 3x2 2 lineáris transzformáció.
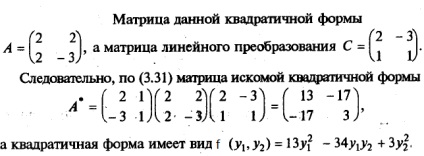
A kvadratikus alak úgynevezett kanonikus (az a kanonikus formában), ha minden együttható aij = 0 i ≠ j, azaz
f (x1. x2. xn) = a11 x1 + A22 x2 2 2 + ... + Ann xn = 2.
A mátrix diagonális.
Tétel (a bizonyítás itt nem szerepel). Bármilyen kvadratikus alak lehet csökkenteni a kanonikus formában egy nem-degenerált lineáris transzformáció.
Ehhez először válassza ki a tökéletes négyzet a változó x1:
Most válassza ki a tökéletes négyzet a változó x2:
Megjegyezzük, hogy a kanonikus formában kvadratikus alak egyértelműen definiálva (egy és ugyanaz a kvadratikus alak lehet csökkenteni kanonikus formában különböző módszerek [1]). Azonban különféle módokon nyert kanonikus formák számos közös tulajdonságait. Különösen a kifejezések száma pozitív (negatív) formájában a másodfokú együtthatók nem függ a redukció eljárása alkotnak ilyen (például, a példában mindig két negatív és egy pozitív együttható). Ezt a tulajdonságot nevezzük a törvény a tehetetlenség kvadratikus formák.
Azt is meg kell jegyezni, hogy a rangsorban a másodfokú formáját nevezzük a rangot a kvadratikus alak. egyenlő a száma nem nulla kanonikus formában tényezők, és nem változik alatt lineáris transzformációk.
Kvadratikus alak f (X) nevezik pozitív (negatív) határozott. ha minden a változók értékeit nem egyenlő nullával ugyanabban az időben, ez pozitív, azaz a f (X)> 0 (negatív, azaz a
f (X) <0).
Például, a kvadratikus alak f1 (x) = x1 2 + x2 2 - pozitív definit, mert képviseli a négyzetösszeg, valamint egy kvadratikus alak f2 (X) = -X1 2 x2 + 2x1 - x2 2 - negatív határozott, mert jelentése lehet képviseletében a F2 (X) = - (x1 - x2) 2.
A legtöbb gyakorlati helyzeteket létrehozni biztos jele a kvadratikus alak némileg bonyolultabb, ezért erre a célra az alábbi tételek (kijelentjük őket bizonyítás nélkül).
Tétel. A kvadratikus alak pozitív (negatív) határozott, ha, és csak akkor, ha az összes sajátérték pozitív mátrix (negatív).
Tétel (Sylvester kritérium). A kvadratikus alak pozitív definit akkor és csak akkor, ha az összes fő kiskorú ebben a formában pozitív.
Fő (szögletes) kisebb K-edik rendű A mátrix n-edik rendű nevezzük meghatározója a mátrix, amely az első k sorok és oszlopok az A ().
Megjegyezzük, hogy a negatív négyzetes formák meghatározott megjelölések fő kiskorúak váltakoznak, az első, hogy a kisebb negatívnak kell lennie.
Például, hogy megvizsgálja a fix jel kvadratikus alak f (x1. X2) = 2x1 + 4x1 2 3x2 + x2 2.
1. módszer: Construct mátrix kvadratikus alak A =. A karakterisztikus egyenlet lesz a forma = (2 - L) *
* (3l) - 4 = (6 - 2L - 3L + l 2) - 4 = L 2 - 5l + 2 = 0; D = 25-8 = 17;
. Következésképpen a négyzetes forma - pozitív definit.
Módszer 2. Fő Minor első, hogy az A D1 = A11 = 2> 0. A fő kisebb másodrendű D2 = = 6 - 2 = 4> 0. Ezért a kritérium Sylvester kvadratikus formában - pozitív határozott.
Vizsgáljuk meg egy másik biztos jele kvadratikus alak, f (x1, x2). = -2x1 + 4x1 2 x2 - 3x2 2.
1. módszer: Construct mátrix kvadratikus alak A =. A karakterisztikus egyenlet lesz a forma = (-2 - l) *
* (- 3l) - 4 = (6 + 2l + 3l + l 2) - 4 = L 2 + 5l + 2 = 0; D = 25-8 = 17;
. Következésképpen a négyzetes forma - negatív határozott.
Módszer 2. Fő Minor első, hogy az A D1 = A11 =
= -2 <0. Главный минор второго порядка D2 = = 6 – 4 = 2> 0. Következésképpen, a kritérium Sylvester kvadratikus alak - negatív határozott (fő kiskorúak alternatív jelek kezdve mínusz).
És egy másik példa, vizsgálja fix jel másodfokú f (x1, x2). = 2x1 2 4x1 + x2 - 3x2 2.
1. módszer: Construct mátrix kvadratikus alak A =. A karakterisztikus egyenlet lesz a forma = (2 - L) *
* (- 3l) - 4 = (-6 - 2l + 3L + l 2) - 4 2 = L + L - 10 = 0; D = 1 + 40 = 41;
. Az egyik ilyen szám negatív, és a többi - pozitívan. Jelek sajátértékek más. Következésképpen a kvadratikus alak nem lehet sem negatív, sem pozitív definit, azaz Ez a tér alakja nem határozott (értékeket vehet bármelyik jel).
Módszer 2. Fő Minor első, hogy az A D1 = A11 = 2> 0. A fő kisebb másodrendű D2 = = -6 - 4 = -10 <0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них – положителен).