Összefoglalás gömb alakú háromszög és annak alkalmazása 2

Gömb Triangle és annak alkalmazása.

Gömbháromszög - geometriai alakja a gömb felülete által alkotott metszéspontja három nagy körökben. Három nagy körök a gömb felülete, amely nem metszi egy ponton képeznek nyolc gömb alakú háromszög. Gömb háromszög minden oldalát, amely kevesebb, mint a fele egy nagy kör, az úgynevezett Euler.

Side gömbháromszög nyugalmi mért érték központi zár be azt. A szög a gömbháromszög mért értéke diéderes szög a síkok közötti amelyben fekszenek oldalán, ez a szög. A kapcsolatok elemei között szférikus háromszögek tanul gömbháromszögtan.

A tulajdonságok a gömb alakú háromszög:

1. Amellett, hogy a három jelei a egyenlőség lapos háromszögek, gömb alakú háromszögek hű még egy, két szférikus háromszög egybevágó, ha azok megfelelő szögek egyenlő.
2. A gömb alakú háromszög oldalai 3 végezzük háromszög egyenlőtlenség: mindkét oldalán kisebb, mint az összege a másik két oldal és több a különbség.
3. Az összeg minden oldalán a + b + c mindig kevesebb 2PR.
4. A mennyiség 2πR - (a + b + c) nevezzük gömb alakú hibája
5. gömb alakú háromszög szögeinek összege s = # 945; + # 946; + # 947; mindig kisebb, mint 3π és π
6. Az érték az úgynevezett gömb vagy gömb feleslegben kurtosis
7. A területet a gömbháromszög képlet határozza meg.
8. Ellentétben lapos háromszög gömbháromszög lehet két, vagy akár három szög 90 ° az egyes.

Között a gömb alakú poligonok legnagyobb érdeklődés a gömb alakú háromszög. Három nagy kört metszik páronként két pont a gömb formájú nyolc gömbölyű háromszög. Ismerve az elemek (oldalai és szögei) egyikük meg lehet határozni az összes többi elemet, azonban figyelembe véve a kapcsolat elemei között egyikük, amelynek kevesebb, mint a fele minden oldalán egy jó kört. oldalán a háromszög mérik lapos szögben háromszög sarokban OABC, háromszög szögei - a torziós szög a háromszög sarokban, lásd az ábrát.

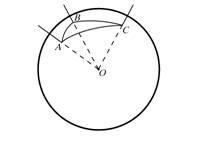
Tulajdonságai szférikus háromszögek különböznek sok szempontból a tulajdonságait háromszögek egy síkban. Így az ismert három esetben egyenlőség egyenes vonalú háromszögek hozzá egy negyedik: két ABC háromszög és A`V`S` egyenlő, ha egyenlő, illetve három szög RA = RA`, PB = RV`, RS = RS`. Így a területen nincsen hasonló háromszögek, sőt, a gömb alakú geometria nem fogalma hasonlóság, hiszen nincs változás, megváltoztatva a távolságokat azonos (nem egyenlő 1) több alkalommal. Ezek a funkciók megsértése miatt az axiómának euklideszi párhuzamos vonalak és a hiperbolikus geometria rejlő. Háromszögek, amelyek azonos elemeket és különböző orientációval, úgynevezett szimmetrikus, így, például, háromszögek és AS`S VSS`

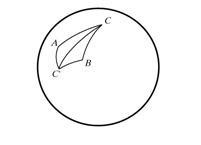
Ha figyelembe vesszük a lune szög, majd 226 = 2p / n (n - egy egész szám) gömb lehet vágni egyenletesen n példányban a lune, és területe a gömb egyenlő 4pR2 = 4p, ha R = 1, így lune területe egyenlő 4P / n = 2a. Ez a képlet az is igaz, a = 2pt / n, és ezért érvényes minden egy. Ha továbbra is az oldalán egy gömb alakú ABC háromszög, és hogy kifejezze a körét a terület révén a területet képez a Lunes szögekkel A, B, C, és a saját területen, akkor lehetséges, hogy jöjjön, hogy a fenti képlet Girard.

Alatt szférikus háromszögek azt jelentette, háromszög a felület egy gömb álló ívek nagy körökben - .. Azaz, azok a körök középpontja a a gömb középpontja. A szögek a gömb alakú háromszög - közötti szög érintők maga mellé, kezében tetejét. Mint általában háromszög szögei változnak 0-180 °. Ezzel szemben a lapos háromszög szférikus szögek összege nem egyenlő a 180 °, és nagyobb, ez könnyen belátható, tekintve, például a háromszög által alkotott ívek két meridiánok és az egyenlítő a világon: a meridiánok konvergál a pole, mindkettő merőleges a egyenlítő, és ez azt jelenti, hogy ez a háromszög két derékszög!

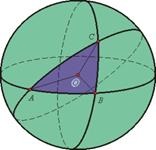
Egy gömb alakú háromszög két derékszög

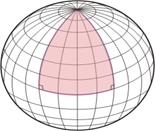
Már van egy indiai Varáhamihira (V-VI-ot.), Az arab matematikusok és csillagászok, mivel a IX. (Sabit Ibn Korra, al-Battani) és a nyugati matematikusok óta Regiomontanus (XV c.), Megtalálható a különböző készítmények figyelemre méltó tétel a gömb alakú háromszögek. Itt van, hogyan lehet kiszerelni a modern jelölés:

cosa = cosbcosc + sinbsinccosA. Gömb koszinusz tétel nagyon fontos a csillagászat és a földrajz. Ez a tétel lehetővé teszi számunkra, hogy összehangolja a két város és B, hogy megtalálják a távolság közöttük. Ezen túlmenően, matematikusok iszlám országokban gömbölyű koszinusz tétel segít megoldani egy gyakorlati probléma: a város a megadott koordinátákat, hogy megtalálják az irányt a szent város, Mekka (minden hithű muzulmán imádkozzunk naponta ötször Mekka felé). Hogy oldja meg ezt a problémát, eltekintve a város Mekka B, meg kellett találni a szög a háromszög.

A csillagászat, gömbölyű koszinusz tétel lehetővé teszi számunkra, hogy adja át az egyik koordináta rendszerben az égi szférában a másikba. Három ilyen rendszereket leggyakrabban használt: az egyik az egyenlítő az égi egyenlítő és a sarkok - pólusai a világon, amely körül van a napi látszólagos elfordulását a csillagok; a másik pedig az ekliptika egyenlítő - egy kört, amelyben egész évben készül látszólagos mozgás a nap a csillagok; harmadik szerepe az egyenlítő teljesíti a horizonton, és a szerepe a pólusok - a zenit és a mélypontját. Különösen, mivel a gömb alakú koszinusztétel lehet számítani a magassága a Nap a horizont felett különböző időpontokban és különböző napokon az év.

Vitorlák Architecture - gömbháromszög, amely egy átmenet egy négyzet a tervben a kupola helyet a kupola a kerülete. Sail, pandativ (a Fr. pendentif.) - része a boltozat a kupola tag miáltal az átmenet a négyszögletes alapja, hogy a kupola mennyezetre vagy annak dob. Sail az alakja egy gömb alakú háromszög, az apex meghajolt le, és kitölti a teret közötti podpruzhnymi ívek összekötő oszlopok a kupola a szomszédos téren. Bázisok gömb alakú háromszögek vitorlák az összeget egy kört kapunk, és a rakományt a kupola kerületének ívek.

Dome a vitorlákat

DzhordzhNelson (George Nelson)

„A tervező kissé pihenni és szórakozni ,. Az eredmény lehet egy vicc, vidám elképesztő, hogy gyakran ez történik nagyon szórakoztató,” Dzhordzh Nelson

Dzhordzh Nelson - amerikai tervező, építész, design kritikus és teoretikus. (1908, Hartford, Connecticut - 1986, New York)

Úgy tervezték, világítótestek, órák, bútorok, csomagolás, részt vesz a kiállítás tervezése.

A leghíresebb tervezési projektek George Nelson képviseli mesteri stilizálás geometriai formák szellemében op art és a geometrikus absztrakció.

Az alakja a híres fekete szék tervező alapul gömb alakú háromszög, széles körben használják az építészeti tervek dóm struktúrákat. Különösen a bizánci templomok és a magyar egy gömb alakú háromszög úgynevezett „vitorla”. Köszönhetően „vitorlázni” a zökkenőmentes átmenetet a kupola a kupola támogatást.

DzhordzhNelson (George Harold Nelson, 1908-1986 gg.)

Koncentrikus sfery.1935g.Tortsovaya gravírozás 24-24 cm.

A használata gömbháromszög:

1. Használata háromdimenziós grafika szférikus háromszögek
2. A csillagászat
3. A földrajz. Tétel gömb alakú háromszög lehetővé teszi a koordinátákat a két város és B, hogy megtalálják a távolság közöttük.
4. A arhitektrue
5. A szék terve George Nelson
6. a gravírozás

Kapcsolódó cikkek

• Gömb Triangle és annak alkalmazása