Négyzetek ázsiai eredetű, a terek európai eredetű, ördögi mágia
Ez az első bűvös négyzet, utalva a különböző úgynevezett ördög négyzetek.
Magic Quadrant Yan Hueya (China)
A 13. században. matematikus Yan Huey vette fel a problémát a módszerek építésének mágikus négyzetek. Kutatásai később folytatta a többi kínai matematikus. Yan Huey tekinthető mágikus négyzetek nem csak a harmadik, de nagy megrendeléseket. Néhány terek meglehetősen bonyolult, de mindig adta a szabályokat az építési. Sikerült építeni egy hatodik érdekében mágikus négyzet, az utóbbi majdnem asszociatív (csak két pár egymással szemben lévő központi számok nem adnak összesen 37) [2]

Négyzetek európai származású
A tér Albrehta Dyurera

Töredék Dürer metszetei „melankólia”
Magic Quadrant 4CH4, ábrázolt metszet Albrehta Dyurera „melankólia I», nem tekinthető a legkorábbi európai művészetben. Két középső szám az alsó sorban azt a dátumot, a teremtés a festmény (1514).
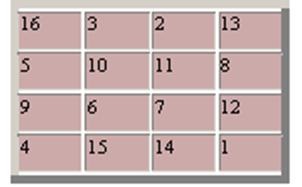
Számok összege bármilyen vízszintes, függőleges és átlós egyenlő 34. Ez az összeg is megtalálható minden a négyzet sarkainak 2CH2, a központi tér (10 + 11 + 6 + 7), a tér a sarok sejtek (16 + 13 + 4 + 1), a négyzetek épített "swing ló" (2 + 8 + 9 + 15 és a 3 + 5 + 12 + 14), a téglalapok által alkotott pár szekunder cellák ellentétes oldalain (3 + 2 + 15 + 14 és 5 + 8 + 9 12). A legtöbb kiegészítő szimmetriák kapcsolódó tény, hogy az összeg a bármely két központilag szimmetrikus elrendezésű szám egyenlő 17.
Négyzetek Henry E. Dudeney és Allan W. Johnson -ml.
Ha egy négyzetes mátrix n × n van rögzítve nem szigorúan természetes számok, akkor a mágikus négyzet - nem konvencionális. Az alábbiakban két ilyen mágikus négyzetek töltött többnyire csak egy szám. Az első a rend n = 3 (Dudeney négyzet); második (méret 4x4) - Johnson téren. Mindkettőt alakult ki a huszadik század elején
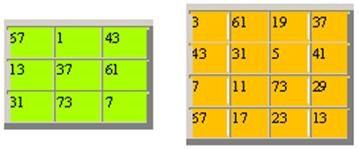
Számos ilyen példát:
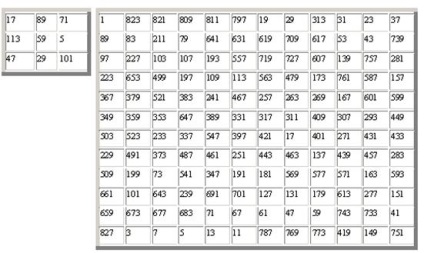
Az utolsó négyzet is figyelemre méltó, hogy ez áll a 143 egymást követő prímszám, kivéve két dolgot: a résztvevő egység, ami nem prímszám, és nem csak használják páros prímszám 2.
Ördög bűvös négyzet
Ördög bűvös négyzet - mágikus négyzet, ami szintén egybeesik a magic constant számok összege törött átlós (diagonális, ami azáltal kerültek kialakításra a tér torr) mindkét irányban.
A négyzetek nevezik több pandiagonalnymi.Suschestvuet 48 4CH4 ördögi mágikus négyzetek akár forgatások és gondolatokkal. Ha figyelembe vesszük egyre szimmetria - tórikus párhuzamos fordítás, akkor lesz csak 3 jelentősen eltérő tér:
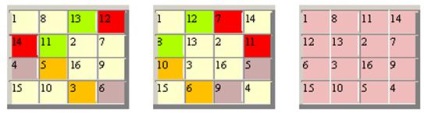
Ugyanakkor bebizonyosodott, hogy az utolsó harmadik lehetőség egyszerűen permutációk kapott számok az első két négyzet. Ez a harmadik lehetőség - ez egy alapvető ördögi tér, ahonnan a különböző átalakításokat lehet építeni az összes többit.
Pandiagonalnye négyzetek a páratlan rendű n> 3, bármilyen sorrendben kettős paritás n = 4k (k = 1,2,3 ...), és nem léteznek egyszeri-paritás-érdekében n = 4k + 2 ().
Pandiagonalnye négyzetének negyedrendű számos további tulajdonságokat, amelyek arra hivatottak tökéletes. Tökéletes négyzetének páratlan rendű nem létezik. Közül pandiagonalnyh négyzetek kettős paritás fenti 4 elkötelezettek. [2]
Pandiagonalnyh ötödrendű négyzetek 3600. Tekintettel tórikus párhuzamos fordítások 144 különböző pandiagonalnyh négyzetek. Egyikük az alábbi ábrán látható.
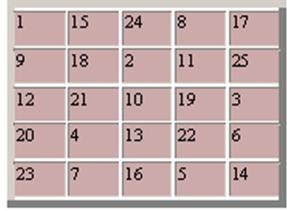
A törött átlós négyzet pandiagonalnogo
Ha pandiagonalny tér is asszociatív, ez az úgynevezett ideális. Egy példa a tökéletes mágikus négyzet:
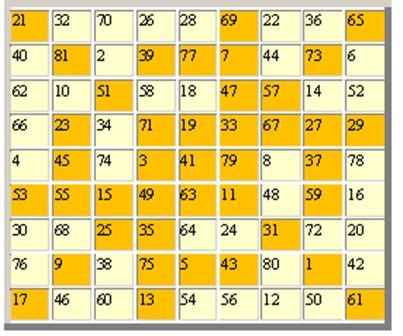
Az eredete a bűvös négyzet elvesznek a sötét középkor. A történelem mágikus négyzetek elválaszthatatlanul kapcsolódik a tudomány fejlődése. Azonban, ha a régi időkben a tér érdekes volt több, mint egy ezoterikus, hogy jelen pillanatban tisztán praktikus. Algoritmusok segítségével töltse mágikus négyzetek volna megoldani bizonyos problémákat a kriptográfia. Azt is megállapította, hogy létezik egy részleges töltet mágikus négyzet algoritmusokat. Általános algoritmus alkalmas minden típusú mágikus négyzetek létezik.