Négyszögek, típusai és tulajdonságai
Quadrangle nevezett ábra, amely négy pont (csúcsok) és négy szegmenst (oldalai), amelyek egymás után összeköti a tetején. Ebben az esetben sem a három adatpontok nem fekszenek egy egyenesen, és összekötő azok szegmensei nem fedik egymást.
Négyszög konvex, ha található egy félig sík vonalhoz képest, hogy tartalmaz-e a felek.
A szögek összege konvex négyszög 360 °:
Nincs quad, amelynek minden szöge akut vagy tompaszög.
Minden sarkából a négyszög mindig kevesebb, mint a másik három szög:
∠A <∠B+∠C+∠D. ∠B <∠A+∠C+∠D.
∠C <∠A+∠B+∠D. ∠ D <∠A+∠B+∠D .
Mindkét fél a négyszög mindig kevesebb, mint a másik három oldala van:
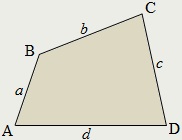
A terület egy tetszőleges konvex négyszög egyenlő:
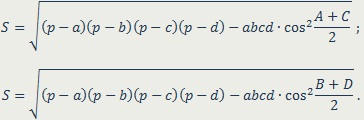
Négyszög átlóival nevezzük összekötő szakaszok átellenes csúcsa.
Átlói metszik konvex négyszög, és egy nem konvex - nincs.
Terület tetszőleges konvex négyszög:
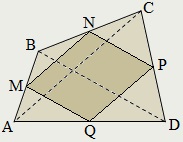
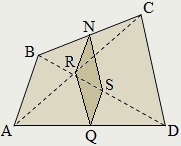
Ha M. N. P. Q - felezőpontja az oldalán egy konvex négyszög ABCD. és R. S - a közepén a átlók, négyszögek MNPQ. MRPs. NSQR a paralelogramma és Pierre Varignon úgynevezett paralelogramma.
Az alakja és mérete paralelogramma Pierre Varignon kapcsolatos alakja és mérete ABCD. Tehát MNPQ - egy téglalap, ha az átlók az ABCD négyszög merőleges; MNPQ - gyémánt, ha az átlók az ABCD egyenlő; MNPQ - box, ha az átlók ABCD merőlegesek és egyenlő;
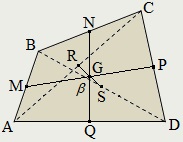
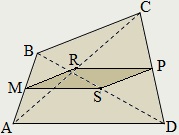
Szegmensek MP. NQ és RS nevezzük első, második, és harmadik középvonalai egy konvex négyszög.
Egy paralelogramma, és csak akkor, a középső az átlók azonos, és ezért a harmadik középvonaltól fajul egy pontot. Más négyszögek középső vonal - szegmenseket.
A másodlagos vonal négyszög metszik egy ponton, és ossza félbe:
A négyzetének összege az átlagos sorban a négyszög negyede a négyzetének összege a minden oldalról és átlók:
MP 2 + NQ 2 + RS 2 = ¼ (AB + BC 2 2 2 + CD + AD 2 + AC 2 + BD 2).
Ha β - közötti szög az első és a második központ vonalak a négyszög, a felület:
SABCD = MP · NQ · sin β.

Egyenlő csempe, amelyek tetszőleges alakúak, nem feltétlenül konvex, a négyszög fedél egy síkban úgy, hogy nincs átfedés a gyűrűk egymás tetején, és a bevonat nélküli részek maradt síkban.
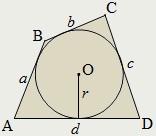
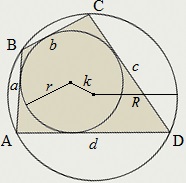
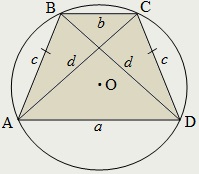
Négyszög úgynevezett leírt a kerülete mentén (a leírt módon), ha létezik egy kör, amely érinti annak minden oldalát, míg a beírt kör maga nevezzük.
Leírjuk, négyszög, ha, és csak akkor, ha az összeg a kódot az ellenkező oldal egyenlő:
Mert le négyszög oldalai és sugara beírható kör hűen:
Leírt négyszög területe:
ahol r - a sugara a beírt kör, p - semiperimeter négyszög.
Leírt négyszög területe:
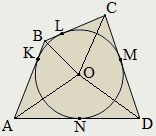
A kör közepén írt a négyszög metszéspontja a szögfelezői a négy sarkából a négyszög.
Az érintési pont a beírt kör van vágva egyenlő szegmensek a szögek egy négyszög:
AK = AN. BK = BL. Cl = CM. DM = DN.
Ha az O - egy kör középpontja a négyzetbe írt az ABCD, majd
∠AOB + ∠COD = ∠BOC + ∠AOD = 180 °.
A leírt ABCD négyszög oldala AB = a. BC = b. CD = c és d = AD igaz összefüggések:
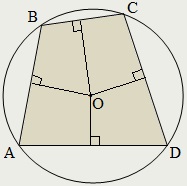
Négyszög úgynevezett beírható kör (feliratos), ha van egy kör áthaladó amelynek csúcsa, majd a kör maga az úgynevezett leírt körülbelül négyszögletes.
A konvex négyszög van leírva, és csak akkor, ha az összeg a átellenes szögek egyenlő 180 °:
∠A + ∠C = ∠B + ∠D = 180 °.
Center leírt kerülete körül a négyszög metszéspontja mind a négy midperpendiculars oldalán a négyszög.
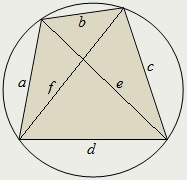
Az első tétel Ptolemaiosz. Konvex négyszög akkor és csak akkor van írva, amikor a egyenlőség:
A második tétel Ptolemaiosz. Konvex négyszög akkor és csak akkor van írva, amikor a egyenlőség:
A kör sugara körülírt a négyszög:
Terület feliratú négyszög:
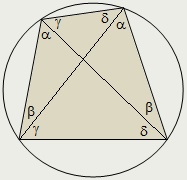
Átlós konvex négyszög Osszuk minden szöget két sarkában. Corners, hajolhat az egyik oldalra, azt mondta, hogy kapcsolódik sarkok.
Konvex négyszög van írva akkor és csak akkor, ha van legalább egy pár egyenlő kapcsolatos szögek.
Mi feliratú négyszög bármely két rokon szög egyenlő.
Ha a négyszög mind le és feliratos, területe:
A sugarak a körülírt és beírt körének a négyszög és a közti távolságot e körök a kapcsolat:
Paralelogramma úgynevezett négyszög, két ellentétes oldalán, amelyek párhuzamosak:
A szemközti oldalán egy paralelogramma egyenlő, és szemközti szöge egyenlő:
∠A = ∠C. ∠B = ∠D.
A összege bármely két szomszédos paralelogramma szög egyenlő 180 °:
∠A + ∠ B = ∠ B + ∠ C = ∠ C + ∠ D = ∠ A + ∠ D = 180 °.
paralelogramma átlói metszik és a metszéspont van felezve:
Minden átlós osztja a paralelogramma két egyenlő háromszög:
∠ ABC = ∠ CDA; ∠ ABD = ∠ CDB.
Két átlója paralelogramma osszuk négy egyenlő háromszög:
A négyzetének összege az átlók paralelogramma egyenlő a négyzetének összege a minden oldalról:
e 2 + f 2 = a 2 + b 2 + 2 2 + b 2 = (a 2 + b 2).
- Ha olyan négyszög, az ellenkező oldalán egyenlő, akkor a négyszög - paralelogramma.
- Ha egy négyszöget a két átellenes oldala egyenlő és párhuzamos, majd a négyszög - paralelogramma.
- Négyszög, amely átlósan egy metszéspont kétfelé osztjuk - egy paralelogramma.
- Ha az ellentétes szögek a négyszög egyenlő, akkor a négyszög - paralelogramma.
A magasság a paralelogramma nevezik merőlegesen végezzük a tetején a paralelogramma neprilezhaschey oldala:
A terület egy paralelogramma lehet meghatározni:
- az ő irányát és magasságát, egyesült, hogy:
- keresztül annak két oldala, és egy szöget közöttük:
S = ab · sin γ.
Trapéz úgynevezett négyszög, amelynek csak két egymással szemben oldalai párhuzamosak:
Párhuzamos oldalai nevezzük bázisok a trapéz, nem párhuzamos - oldalát.
A magasság a trapéz - merőleges által végzett tetszőleges pontja bázis a trapéz, hogy egy sort tartalmazó különböző bázis a trapéz.
A középső sor (az első középső vonal) nevezzük trapezoid szegmens, amely összeköti a felezőpontja az oldalán a trapéz:
A középső sor a trapéz párhuzamos, hogy az alap, és a felével egyenlő az összege:
KL = ½ (AD + BC).
A tovább folytatott amíg keresztezi az oldalán a trapéz képez két hasonló háromszögek a hasonlósági faktor arány egyenlő a bázisok:
δ AED ∼ δ BEC. k = AD / BC.
Háromszögek által alkotott elvek és átlós szegmensek egy hasonlósági faktor arány egyenlő a bázisok:
δ AOD ∼ δ COV. k = AD / BC.
Területek háromszögek által képzett oldalai és átlóinak trapéz szegmensek egyenlő:
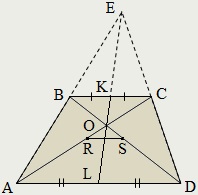
Szegmens összekötő közepén a bázis (a második középső sorban) trapéz, áthalad a metszéspontja az átlók, és annak meghosszabbítását - metszi a kiterjesztések oldalainak:
Összekötő szakasz felezőpontja az átlók (harmadik középvonala) a trapéz, és párhuzamos a bázisok azok félig:
RS = ½ (AD-BC).
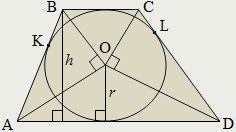
A trapéz kör írható, ha az összege alapján az összege az oldalán:
Központja a beírt kör a trapéz a metszéspont a szögfelezői belső szögeinek trapéz.
Egy trapéz ABCD bázisokkal AD és BC lehet helyezni egy kört, ha, és csak akkor, ha megfelel legalább az egyik az egyenletek:
Az oldalán a trapéz látható a közepén a beírható kör trapéz, derékszögben,
∠ AOB = ∠ COD = 90 °.
A kör sugara írt a trapéz lehet meghatározni:
- keresztül a szegmensek osztani az oldalsó oldala az érintkezési pont:
Ez az úgynevezett egyenlő oldalú trapéz, amelynek oldalai egyenlő:
Az egyenlő oldalú trapéz:
- szögek a bázis:
∠ A = ∠ D. ∠ B = ∠ C;
- összege szemközti szögek 180?:
∠A + ∠ C = ∠ B + ∠ D = 180 °.
Mintegy trapéz lehet leírni, mint egy kör, ha és csak akkor, ha egyenlő szárú.
Pártok és átlós egy egyenlő oldalú trapéz kapcsolódnak:
Trapéz nevezett téglalap alakú, ha egyik oldala merőleges a bázis.
A terület trapéz lehet meghatározni:
- a fél összeget a bázisok (első középső sor) és a magasság:
- az átlós és a köztük lévő szög:
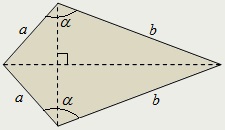
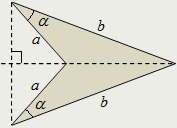
Deltoid úgynevezett négyszög, amelynek két szomszédos pár egyenlő oldala.
Deltoid lehetnek konvex vagy nem konvex.
Közvetlen bármelyikét tartalmazó diagonális deltoid metszik derékszögben.
Mindenesetre deltoid közötti szögek szomszédos oldala egyenlőtlen.
A terület bármely deltoid lehet meghatározni:
- két egyenlőtlen szomszédos oldalán, és egy szöget közöttük:
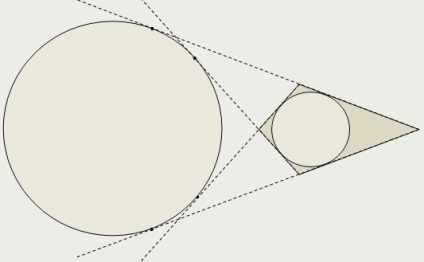
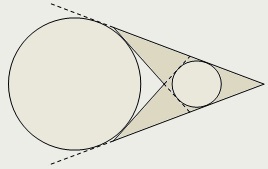
Mindenesetre konvex deltoid lehet helyezni egy kört.
Ha domború deltoid nem a gyémánt, van egy kör érinti a kiterjesztések mind a négy oldalán a deltoid.
A nem-konvex deltoid lehet építeni egy kör érintő két oldalán nagyobb a hosszúsága, a meghosszabbításai két kisebb fél, valamint a kör érintő a két kisebb fél és a nyúlványok két oldalának nagyobb hosszúságú.
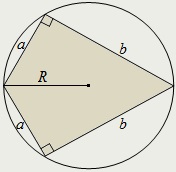
Mintegy deltoid képes leírni egy kört, akkor és csak akkor, ha az egyenlőtlen fél alkot szögek 90 °.
A kör sugara körülírt a deltoid lehet által meghatározott két egyenlőtlen fél:
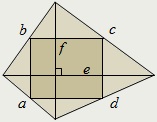
Négyszög úgynevezett ortodiagonalnym ha átlói metszik derékszögben.
Négyszög ortodiagonalnym akkor és csak akkor, ha az megfelel az egyik feltétel:
- az oldalán a négyszög igaz: a² + c² = b² + d ²;
- a négyszög területe igaz: S = ½ef;
- Pierre Varignon paralelogramma csúcsot a felezőpontja az oldalán a négyszög téglalap.
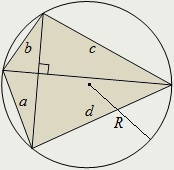
Négyzetösszege ellentétes oldalán a beírható kör a négyszög ortodiagonalnogo egyenlő a négyzetes átmérője a körülírt kör:
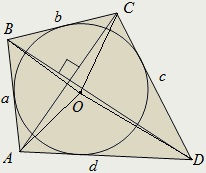
Ortodiagonalny négyszög leírt kerülete körül, ha, és csak akkor, ha a terméket annak ellentétes oldalain mértéke:
Ha ABCD - ortodiagonalny négyszög körülírt egy kör középpontja O ponthoz Az arány az igaz:
Hosszú I tervezett és végre! Olyasmi, mint ez a történet a mi csoport VKontakte. Kétségei vannak a szükségességét annak létezését dobni, és az első anyag közösség lefektetett.
Ez kiterjeszti a funkcionalitást a főmenübe.