N Save edik és k-és kiterjesztem-CIÓ és idő
Conservation törvények és szimmetria térben és időben.
17.1. Conservation törvényeket.
Megvizsgáltuk a három megmaradási törvények, futás zárt rendszerek: a törvényi energiamegmaradás, lendület és perdület.
A mechanika (fizika, minden) koordinálja, és a sebesség függvénye, amelyek megtartják a mozgás állandó értékek, és csak attól függ a kezdeti feltételek, az úgynevezett integrálok mozgás.
Azonban nem minden a integrálját mozgás mechanika játszanak egy ugyanilyen fontos szerepet. Köztük van három. amelyeknek az eredete mély fizikai jelentése: azok kapcsolódnak az alapvető tulajdonságait a tér és idő - ezek homogén, izotróp. Mindezek a megmaradó mennyiségek fontos közös tulajdon - adalékanyag. azaz a fontos, hogy a rendszer, amely a részek, a kölcsönhatás elhanyagolható (ez nem befolyásolja a mozgás folyamat) az összege értékeket minden alkatrészt. Az említett adalékanyagot tulajdonság lehetővé teszi számunkra, hogy vizsgálja meg értékeket a játék a mechanika egy kiemelkedően fontos szerepet.
Nagyon gyakori állítás, hogy a törvények természetvédelmi következménye a homogenitás és izotrópiájára térben és időben. Azonban hiba lenne azt gondolni, hogy csak a megadott tulajdonságait a tér és idő elég ahhoz, hogy ezek a védelmi törvényeket. Mindezek a törvények következtében a törvények a mozgás (pl 2. törvénye Newton). Ezért a vásár a következő nyilatkozatot:
megmaradási származhat Newton 2. törvénye, ha figyelembe együtt a szimmetria tulajdonságai térben és időben.
17.2. A szimmetria térben és időben.
A szimmetria a tér és idő, megértjük a homogenitás a tér és idő, valamint az izotróp térben. Mi a homogenitás az idő, a tér és izotrópiájára tér? Mi magyarázza, mit jelent fektetett ezeket a fogalmakat.
1) egységessége idő azt jelenti, hogy ha két időpont valamennyi szerv a zárt rendszer tegye pontosan ugyanolyan körülmények között, de kezdve ezeket a pillanatokat, minden jelenség ebben a rendszerben folytatódik ugyanúgy.
2) egységessége hely azt jelenti, hogy ha egy zárt rendszerben a testek mozgatni egyik helyről a helyet egy másik is, mivel az összes testet benne, ugyanolyan körülmények között, amelyben voltak ugyanabban a helyzetben, ez nem befolyásolja a tanfolyam későbbi események.
3) izotrop hely azt jelenti, hogy ha egy zárt rendszerben a testek térbeli forgatni bármilyen szögben, mialatt az összes testet benne, ugyanolyan körülmények között, amelyben voltak ugyanabban a helyzetben, ez nem befolyásolja a tanfolyam későbbi események.
Ezek a tulajdonságok a tér és az idő - az alapvető általánosítása kísérleti tényeket.
17.3. A homogenitás a tér, és a törvény megőrzése lendület.
Tehát, mivel a homogenitása mechanikai tulajdonságainak egy zárt rendszer nem változott a párhuzamos közlekedési rendszer egészének a térben.
Vigyük át a rendszer egy tetszőleges pozícióban
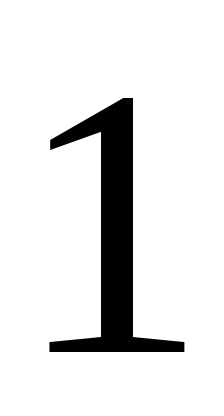
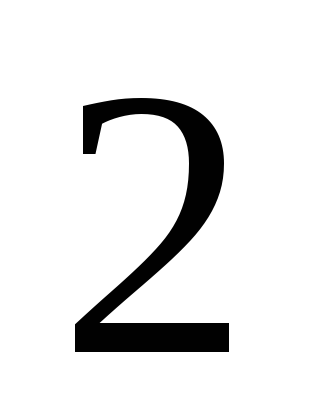
Működési zárt villamosenergia-rendszer
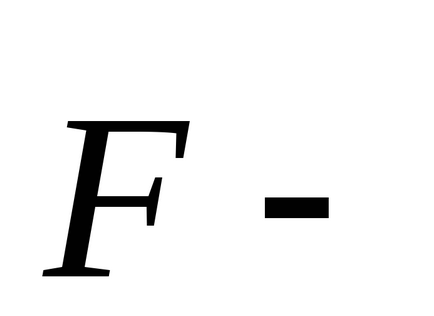
Mivel a hely egységes, amikor a transzfer az összes részecske a rendszerben a térben az azonos távolságra
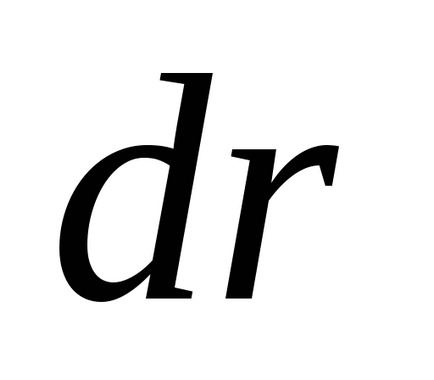
bármely
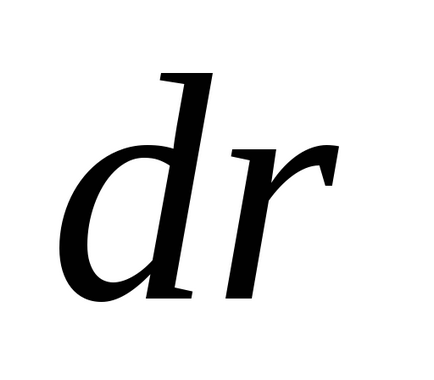
.
Ezután Newton második törvénye lendületmegmaradás kapjuk:
A fenti vita, ez is egy fontos eredmény.
Mivel az összeg az összes erők egy zárt rendszerben nulla, akkor tudjuk írni
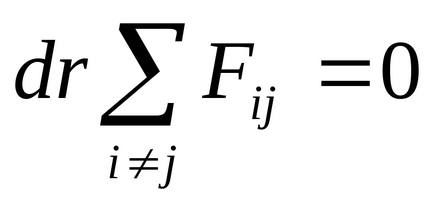
ahol
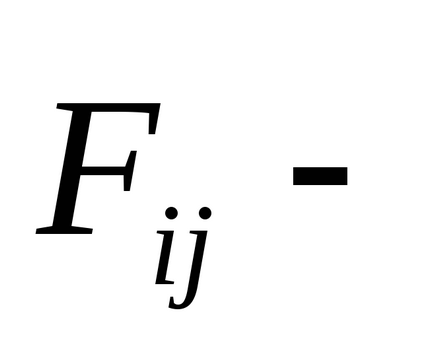
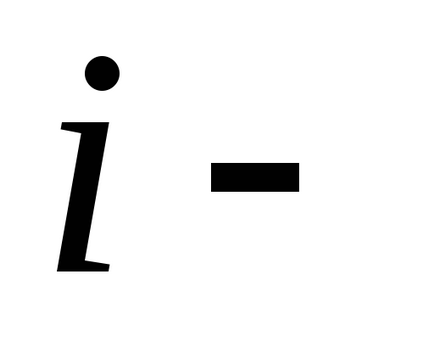
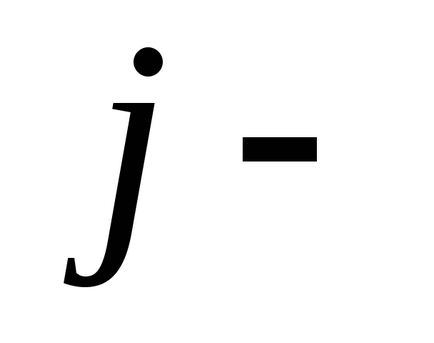
Átírása ez a feltétel másképp
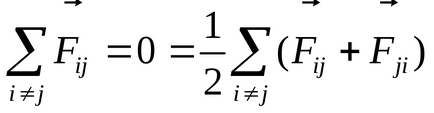
tekintettel a függetlenség minden kölcsönhatásának pár részecskék egymással megkapjuk a harmadik törvény Newton:
Egy zárt rendszerben a törvény lendületmegmaradás következik formálisan a 2. törvénye Newton, ha azt feltételezzük, hogy minden színészi erők figyelemmel a törvény az akció és reakció erők (a harmadik törvény Newton).
Ugyanakkor a végrehajtás a harmadik törvény Newton, valamint a törvény megőrzése lendület, obuslovlenyodnorodnostyu helyet.
Megjegyzés. Ha az impulzus fuvarozók nem csupán anyagi test, hanem a területen, a harmadik törvény Newton ezen készítmény nem alkalmazható.
Ugyanakkor, figyelembe véve a hozzájárulást a területen, zárt rendszer szerveinek homogenitását tér, megint kap a törvény lendületmegmaradás:
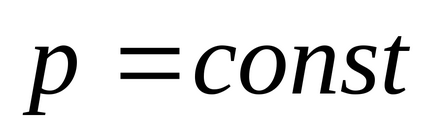
17.4. Izotrópiájára tér és a törvény védelme perdület.
A izotrópiájára hely azt jelenti, hogy forgása során a zárt rendszerben bármilyen szögben tér ebben a rendszerben nem lesz változás.
Egy zárt rendszer testek külső nyomatékok
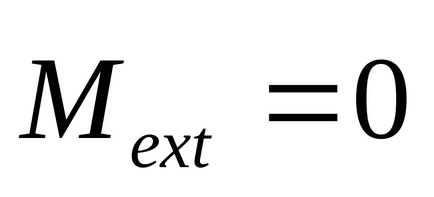
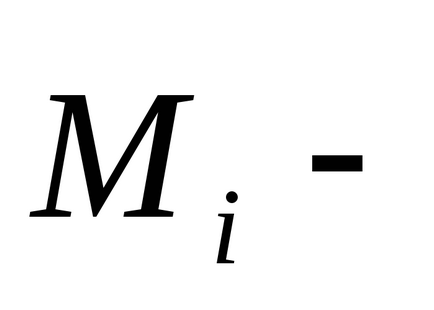
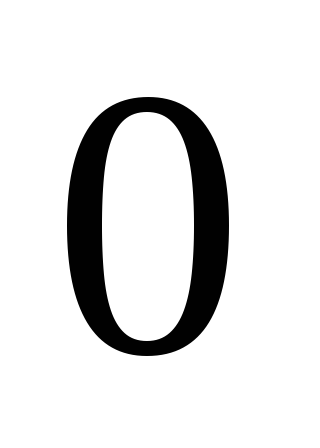
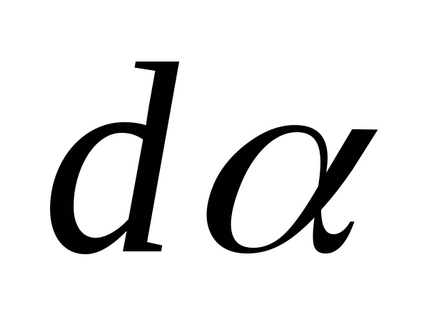
Due izotrópia helyet a rendszeren belül nincs változás ebben a megfordítása nem fordul elő, azaz, a munkaerő a rendszeren belül működő nullának kell lennie:
.
Tekintettel az önkényesség a szög
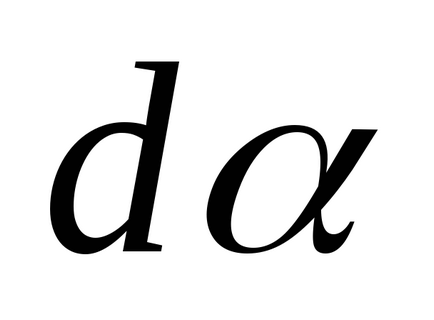
És ebből következik a törvény megőrzése perdület:
17.5. A törvény az energiamegmaradás és a homogenitás az idő.
Figyelembe véve a problémákat, a dinamika, megvan az eredménye a 2. törvénye Newton - a munkaerő, kész a mechanikai rendszert, ez egyenlő a növekmény a kinetikus energia:
Mi kell első szempont vonatkozásában egy ponton az anyag.
bevall
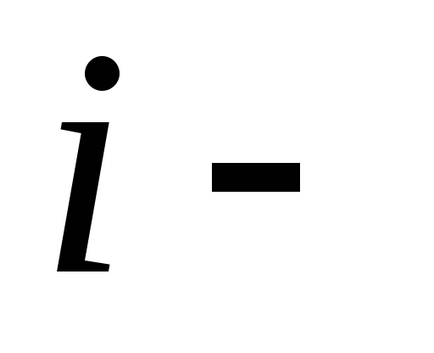
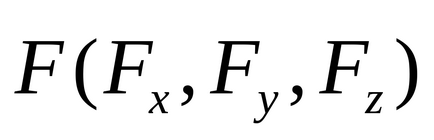
A legáltalánosabb esetben a potenciális energia (például, az egy nyitott rendszer) esetenként nemcsak a koordinátákat, de még mindig időben: a teljes növekmény és potenciális funkciót is tartalmaz, egy időben származékának (azaz a differenciál bevezetésének teljes 4 változók ):
Végén a mozgó anyag pont pozíciót
Egy zárt rendszerben szervek munkáját az erők, amelyek mozognak az integrál
hozzá, és kivonni a jobb oldalán a parciális derivált adott időben, akkor
Összefoglalva az egész anyagot pontokat a rendszer, megkapjuk a egyenlőséggel kapcsolatos munka
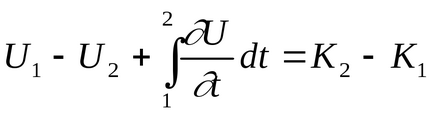
Ez az eredmény is érvényes nyílt rendszerek.
Hivatkozva ismét a zárt rendszer a testek és használja az ingatlant homogenitása időben.
Egységessége idő, hogy kezdve bármely időpontban az események kell bekövetkeznie ugyanúgy, azaz A homogenitás idő a potenciális energia a zárt rendszer testek (tömeg pont) nem kifejezetten az időtől függenek
Ebből ered az a törvény az energiamegmaradás:
Ahelyett, hogy a következtetést. dinamikus egyenletei és megmaradási tételek lényeges különbség.
dinamika törvényei adnak részletes képet a folyamatot. Megmaradási törvények által okozott alapvető tulajdonságai a tér és idő, és így azok általános és átfogó. De nem ad részletes útmutatást a fejlődés egy folyamat. Azt mondják, csak arról, hogy mit folyamatok tilos a természetben. Megmaradási törvények hatnak korlátozások (korlátozások)! Ha például úgy tűnik, hogy néhány folyamat ellentétes a jogszabályok megőrzése, azonnal állítható, hogy ez a folyamat lehetetlen és értelmetlen, hogy megpróbálja végrehajtani.