Mordkovich 18. §

18.1. Keresse meg a számot is:
a) kétjegyű szám;
b) kétjegyű szám, amely a különböző számjegy;
c) kétjegyű szám, az összeget a számjegyek nagyobb, mint 16;
g) kétjegyű szám, amelynek terméke kevesebb, mint 2 számjegy.

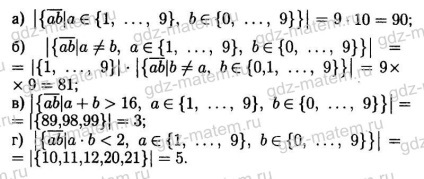
18.2. A számok 4, 6, 7, amelyek között különböző háromjegyű számok ismétlése nélkül számjegy.
a) Mekkora a legnagyobb számban.
b) Mekkora a legkisebb számot, amelynek második számjegy 7.
c) Hány szám végződik a 7. ábrán lehet együtt fogadást?
g) Hány szám képezhető?

18.3. A számok 0, 1, 4, 8, 9 képez egy kétjegyű számot (ismétlés-szám engedélyezett).
a) Mekkora a legnagyobb számban.
b) Mekkora a legkisebb szám, amely osztható 9.
c) Hány páros számok képezhető?
g) felsorolni az összes szám, amely többszöröse 8.

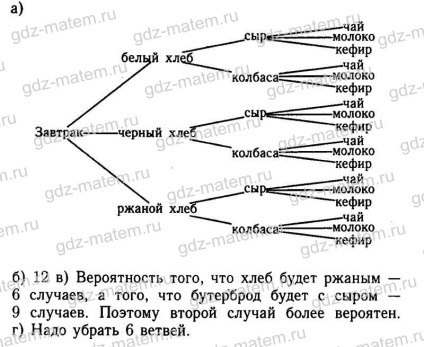
18.4. Reggeli egy darab fehér, fekete vagy rozskenyér tudunk sajt vagy kolbászt. Sandwich lemosható tea, tej vagy joghurt.
a) Rajzolj egy fát a lehetséges opciókat a reggelit.
b) tejital lesz kiválasztva hány esetben?
c) Melyik a valószínűbb: hogy a kenyér rozs, vagy mi fog történni a sajtos szendvicset?
d) Hogyan lesz a fa lehetőségeket, ha tudjuk, hogy a sajt kerül fekete kenyeret és kolbászt nem fog inni kefir?

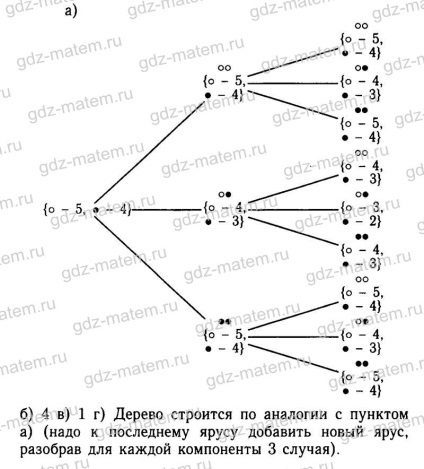
18.5. Egy urnában fekszenek kilenc megkülönböztethetetlen érintéssel labda: öt fehér és négy fekete. Vegye ki a két golyó egyszerre. Ha ezek a különböző színű, ők félre, és ha ugyanazt a színt, majd visszatért az urnát. Ezt a műveletet még kétszer megismételjük.
a) Rajzolj egy fát lehetőségeket.
b) Hány esetben lesz kilenc golyó az urnában?
c) Hány esetben az urna nem lesz több, mint öt golyó?
g) Rajzolj egy fát a lehetséges opciókat, ha a meghatározott feltétel a műveletet háromszor megismételjük.

18.6. A folyosón három izzók.
a) Hányféleképpen világítás a folyosón, ideértve azt az esetet, amikor az összes lámpa ki van kapcsolva?
b) Hányféleképpen a világítás, ha tudjuk, hogy izzók 1-es és 2-es szám világít vagy nem világít ugyanabban az időben?
c) Hány különböző módon a világítás, ha ismert, hogy az égő villanykörte lámpa 3-as szám a 2. számú nem világít?
g) Hányféleképpen világítás a folyosón, ha világít, a legtöbb izzók?

18.7. Számos ország úgy döntött, hogy a nemzeti zászló téglalap négy függőleges sáv szélessége azonos a különböző színek: fehér, kék, piros, zöld. Minden országban - a zászló. Hány ország:
a) lehet használni az ilyen zászlók;
b) használhatják zászlók az első fehér sáv;
c) lehet használni a harmadik zászlók nem zöld csíkkal;
g) lehet használni egy kék zászlók piros csíkos elrendezve egy sorban?

18.8. A kifestőkönyv húzott diszjunkt háromszög, négyzet és kör. Minden szám kell festeni az egyik a szivárvány színeit, különböző számok - különböző színekben.
a) Hányféleképpen vannak, hogy festmény?
b) Hányan vannak azok, hogy körbe - Orange?
c) Hányan vannak azok, amelyekben a háromszög - nem piros?
g) Hányféleképpen vannak, hogy lehet színes hideg színek?

18.9. A koordinátasík megjelölte az összes pont, az abszcissza és ordináta amelyek az alábbi számokkal: -3, -1, 1, 2, 7 (ismétlés megengedett).
a) Hány ilyen pontokat?
b) Hány pontot feküdjön a bal oldalon az y tengely?
c) Hány pontot felett van az x-tengely?
g) Hány pontot fekszenek egy 5 egység sugarú kört középpontú a származási?

18.10. Ismeretes, hogy x = 2a3b5s és a, b, c - a szám a több (véletlen engedélyezett).
a) Mekkora a minimális és maximális értékei x.
b) Hány ilyen szám képezhető?
c) Hányan fognak páros számok?
g) Hány ilyen szám lesz null megszűnik?

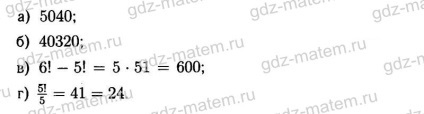
18.13. Van osztva 11! on:
a) 64; b) 25; c) 81; d) 49?

18.15. Problémák a pozitív egész számok a következő egyenletet:
! A) n = 7 (n - 1)!; c) (k - 10)! 77 = (k - 11)!;
b) (M + 17)! = 420 (m + 15)!; g) (3x)! = 504 (3x - 3)!.

18.16. érkeztek vendégek A, B, C, D. A kerekasztal a tulajdonos a ház - öt különböző székek.
a) Hányféleképpen vannak ülőhely?
b) Hányféleképpen vannak ülőhelyek, ha a hely már ismert a ház ura?
c) Hányféleképpen vannak ülőhelyek, ha tudjuk, hogy a vendégeket kell mellé a vendég Ap
g) Hányféleképpen vannak ülőhelyek, ha tudjuk, hogy egy vendég nem szabad ültetni közelében vendége D?

18.17. A 0, 2, 8, 9 alkotnak különböző háromjegyű számot (megengedett számú ismétlés).
a) Határozzuk meg a legkisebb számot.
b) Adja meg az összes számot, amelyek kevesebb, mint 250 mm.
c) Határozza meg minden páratlan szám nagyobb, mint 900.
d) Sorolja az összes számot, amely többszöröse a 40.

18.18. Az alján a portfolió megkülönböztethetetlenek tapintású toll: két egyszerű és három színes. Diák veszi ki őket egyesével. Szüksége van színes ceruzák és egy ceruza feltárt küldi vissza az alsó a portfolió, és színes levelek az asztalra. Ezt a műveletet háromszor megismételjük.
a) Rajzolj egy fát lehetőségeket.
b) Hány esetben, minden lefektetett ceruzák egyszerű lesz?
c) Hány esetben, minden lefektetett színes ceruza?
d) Hány esetben között színes ceruzák lefektetett, hogy több mint egyszerű?

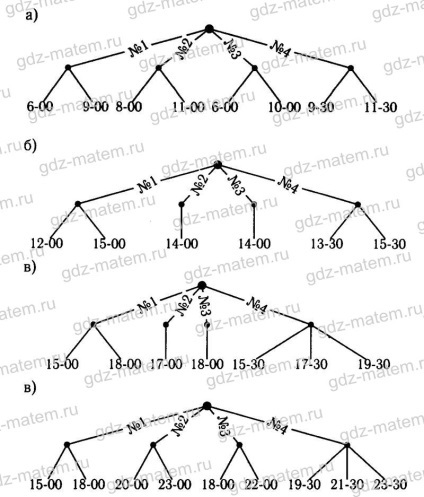
18.19. Az alábbi táblázat tartalmaz információt a kimeneti hírek négy TV csatornák.
Azt akarod, hogy válasszon egy sajtóközleményben. Rajzolj egy fát lehetséges választások közötti időszakban:
a) 11-45, hogy 6-00; c) 15-00 a 19-45;
b) 12-00 a 15-45; d) 18-00 a 23-45.

18.20. Tanár készülni vizsgálatok négy problémák megoldására lineáris egyenlőtlenségek, öt szót problémák (kettő a mozgás és a három munkahelyen) és hat feladatok megoldása másodfokú egyenlet (két feladat diszkrimináns negatív). Az ellenőrzés legyen probléma mindhárom témákról. Keresse meg a számát:
a) az összes lehetséges ellenőrzési eljárásokat;
b) azokat a lehetőségeket, amelyek megfelelnek a probléma a mozgás;
c) ezeket a lehetőségeket, amelyek egy másodfokú egyenlet legalább egy gyökere;
g) azokat a lehetőségeket, amelyek nem felelnek meg egyidejűleg a feladat, hogy a munka és a másodfokú egyenlet, amelynek nincs gyökere.

18.21. Az ellenőrzés lesz öt feladat: az egyik az öt témát telt el. Az egyes témáknál, a tanár által készített lista a tíz feladatot. Köztudott, hogy a vezérlő lesz kihívás ezekből a listákból. Az egyes témáknál, a tanuló képes megoldani nyolc problémák és nem tudja megoldani a két problémát. Keresés:
a) az összes az összes vezérlési lehetőségeket;
b) A választási lehetőségek száma, amelyben a hallgató képes megoldani az összes öt célkitűzés;
c) a számos lehetőség, amelyben a hallgató nem oldja meg minden problémát;
g) a lehetőségek száma, amelyben a hallgató képes megoldani minden problémát, kivéve az elsőt.

18,22. Ismeretes, hogy x = 2aZb5s és a, b, c - a számos különböző készletek.
a) Mekkora a minimális és maximális értékei x.
b) Hány ilyen szám képezhető?
c) Hányan lesznek páratlan számok?
g) Hányan lesznek többszöröse 12?

18.23. a) pont (0, 0), (2, 0), (3, 2) vannak, a háromszög csúcsait. Hányféleképpen lehet kijelölni a tetején a levelek A, B, C?
b) pont (0, 0), (0, 4), (3, 0), (3, 7) a csúcsai a trapéz. Hányféleképpen lehet kijelölni a tetején a levelek K, L, M, N?
c) A pontok (1, -3), (0, 0), (0, 4), (3, 0), (3, 7) vannak csúcsai egy konvex ötszög. Hány módon határozza meg ezeket a csúcsokat betűk P, R, S, T, Q?
d) Hány esetben a munkát) PR egyik fél?

18.24. A röplabda csapat hat embert, és a helyszínen hat találat (számok) az elhelyezést.
a) Hányféleképpen a csapat maradhat a helyén?
b) Hányféleképpen vannak helyek, ahol a kapitány a pályán?
c) Hányféleképpen az elrendezés, amelyben a kapitány nem a pályán?
g) Hányféleképpen vannak helyek, ahol a kapitány vagy a pályán, vagy a helyén egy pont őr?

18.25. Egyszerűbb a kifejezést: