Miért nem lehet nullával osztani, és akkor szaporodnak
Bizonyítja élénken. A burgonya.
Vegyünk egy burgonyát. Ez az, amit szorozva 1. Itt egyedül volt.
Vegyünk két katofeliny. Ez azt megszorozzuk 2 kap két.
Vegyünk öt burgonya. Ez krumpli, mi megötszöröződött.
Vegyünk két alkalommal öt burgonya. Ezt megszorozzuk 2-5.
Burgonya szorozzuk nulla. Vedd hányszor? Ez igaz, nulla. Azaz, ne vegye egy ideig.
Most osztódnak. Vegyünk egy burgonya (egység) és osztódnak.
Először egy részét. Murphy maga egy részben érintetlen marad.
Osszuk meg 2. Chirk kést - már két fele burgonya.
Cserélje az egész osztva 3 vágjuk három részből áll.
Hogyan nullával osztani alkatrész? Nos, ezt a részt nem létezik? Semmi.
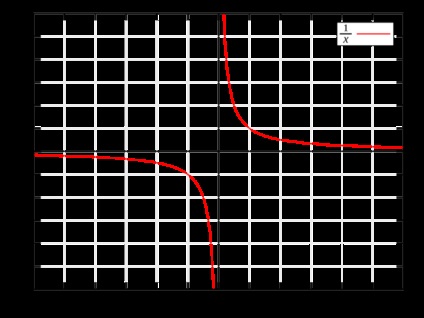
Ez a grafikon a függvény y = 1 / x, ami azt mutatja, hogy a megközelítés, hogy a nulla Xs y megközelítések plusz vagy mínusz végtelen. De végtelenhez - egy darab, így például törekedtek, még kicsi, így az eredmény nem definiált.
A hasadási folyamat van osztva egy bizonyos számú részvényt, ha nulla lebeny osztály elveszti értelmét - időpocsékolás. De a szorzás folyamat egy másik karakter - és megmutatja, hogy mennyi időt kell adni a számot. Ha nem, az eredmény megfelelő. Zero számos általános mágia és úgy tűnt, érdekes - először a példák csak elhagyta egy üres hely, de ez nem volt túl kényelmes. Sőt, az egyik fogja hagyni több helyet, mint mások, és a körülmények kényszerítették, hogy kerek a hely üres volt.
Aztán megint, ha azt mutatja, hogy hányszor kell megállapítani, ha pl 23 halom 0 alkalommal (azaz egyáltalán nem), akkor a szám nem fog hajtani, és marad 23. A szabályok szerint a szorzás 0 lesz Könnyebb lenne betiltani szorozni 0. Noha a gyanúsított szorzás 0 fűzött hogy könnyebb elvégezni aritmetikai számítások, de nem biztos. - 2 éve
Dundee nem igaz. Ha „szeres” nulla idő, semmi sem maradt, mint akárhány, ugyanaz 23, például, meg kell tenniük nulla idő. Vagyis semmit tenni. Ha van valami balra, az azt jelenti, hogy nem kell szorozni nulla. Hányszor kell venni 23-23 kiderült? - 2 éve
Nos, ez mind történik a valóságban.
Ha van (például) tíz almát, akkor könnyen szét őket (például) tíz ember. De ha ugyanaz a tíz alma, és a nulla emberek, akkor nem lehet felosztani. Mert ahogy oszthatjuk az almát, ha nem azok, akikre ők is adnak?
Nos, szorzás nullával, elvileg lehetséges. Mert az életben ez azt jelenti, hogy valamit, egy bizonyos számú alkalommal. Akkor például, gyalog tíz egymást követő napon, egy halászati út. És minden egyes alkalommal, hogy utolérjék tíz ponty. És így, a halakat, a száma száz darab. Vagyis, mi tízszer tíz, és kapott egy száz. De ha megy a folyó tíz napig, és nem fogni a legkisebb halat, akkor kap egy nulla eredményt. Amit alátámaszt matematikailag. Tíz szorozva nulla nulla.
Így azt találtuk, hogy nem lehet nullával osztani, és szaporodnak - amennyire csak lehetséges. Annak ellenére, hogy használhatatlan.