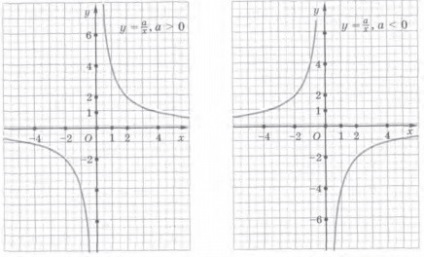
Mi túlzás, mi a tulajdonságok és a menetrend
Funkció képlettel definiált y = A / X. ahol x - az érvelés, és - egy bizonyos számú nem nulla, az úgynevezett fordított arányosság. A tartomány ezen funkció - a készlet minden valós számok, kivéve a 0. számú Valójában, ha az x értéke megfelel annak a feltételnek x ≠ 0, a kifejezés a / x beállítása.
Megjegyezzük, hogy a 0 szám nem a domain a funkció y = a / x. másnak menetrend nem tartozik a ponton az abszcissza nullával egyenlő, azaz a. e. A grafikon metszi az y tengelyen. Mivel bármelyik értéke az érv x, y értéke nem nulla, a grafikon nem metszi az x tengelyt.
Ha az érték az érvelés x pozitív, akkor a y értéke szintén pozitív, ugyanabban az időben növekvő pozitív értékek a argumentum x y értéke csökken, és kevesebb is lehet, mint bármely előre kiválasztott kis számú. Ez azt jelenti, hogy a növekedés a pozitív értékek az érvelés x pont a függvény grafikonját egyre közelebb az x tengely, de soha nem kerül.
Közelítő pozitív abszcissza nulla teszi a függvény értéke egyre nagyobb. Ez azt jelenti, hogy csökken az értéke az argumentum x pont a függvény grafikonját egyre közelebb az y tengelyen. de soha nem keresztbe.
Hasonlóan viselkedik diagram és negatív értékeket, amikor az érvelés. Ha az érték az érvelés x negatív, akkor a y értéke szintén negatív, míg a növekvő modul negatív értékei az érv x egységnyi értéke y csökken, és kevesebb is lehet, mint bármely előre kiválasztott kis számú. Ez azt jelenti, hogy a növekedés a modulus a negatív értékek az érvelés x pont a függvény grafikonját egyre közelebb az x tengely. de soha nem keresztbe.
Közelítő negatív abszcissza nulla függvény értékei modullal nagyobb és nagyobb. Ez azt jelenti, hogy csökken a modulus értékeit az érvelés x pontra a grafikonon a funkció egyre közelebb az y-tengelyen. de soha nem keresztbe.
A grafikon a fordított arányosság nevezzük hiperbola. Ezzel szemben a közvetlen arányosság grafika, hiperbola két részből áll, az úgynevezett ága a hiperbola.
Általában, ha a> 0, a hiperbola ágak az első és a harmadik negyedévben. Ha egy <0, то ветви гиперболы находятся во второй и четвертой координатных четвертях.