Mértani sor - studopediya

Ez egy mértani haladvány első tagjai, nevezők

A összege az első n feltételei Egy mértani

Mint tudjuk, az iskolai tananyag, az összeg az első n-feltételei Egy mértani

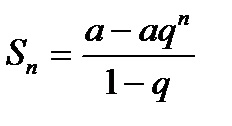
A képlet az n-edik tag

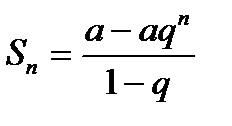
Képzeljünk el egy néhány esetben, amikor

1. Ha igen, akkor mikor

Tehát abban az esetben a sorozat (15,4) konvergál és összege

2. Ha az idő és

azaz, hogy nem létezik. Így. abban az esetben, (15.4) divergál.

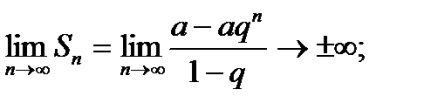
3. Ha q = 1, akkor a sorozatot (15.4) formájában A + A + A + ... + a + ...

Vagyis a sorozat eltér.

4. Ha q = -1, akkor a sorozatot (15.4) rendelkezik formájában A-A + A-A + A- ... + a- ...

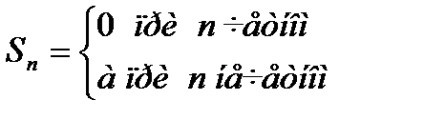
Ennélfogva nincs határa, a sorozat eltér.

Mi a mértani haladvány az első ciklus. nulla konvergál, ha a nevező a progresszió abszolút értéke kisebb, mint egység.