Megoldási módjait, egyenletrendszerek
Tervezésekor kívüli tevékenységek, azt a célt tűzte ki: felhívni a diákok érdeklődését a téma iránt. Választani hozzájárulnak a matematikai kilátások, a kreatív képessége a tanuló, elősegítve a készségek önálló munkára, és ezáltal a minőségi matematikai előkészítése a hallgató.
Ez választható kurzus tartotta a 9. évfolyamon tanulmányozása után témákat, mint a repeater-szintézis, amely lehetővé teszi, hogy ne csak összefoglalja és megszilárdítani tudásukat. Ezen az ülésen is meghívott 10 résztvevő 7 osztály, amelyben dolgozom (köztük 2 társelőadó).
Tárgy: „Methods megoldására egyenletrendszerek.”Típusa lecke - egy sajtótájékoztatón.
- Keresése különböző módokon és megoldási módjainak egyenletrendszerek, képes beszélni, hogy a közönség egy előkészített üzenetet.
- serkentik a kreatív gondolkodás nem szabványos módszerek.
- általánosítás és rendszerezése a diákok tudásának a témában, tanítani munka segítségével és további irodalom.
- fejlesztése a matematikai gondolkodás, a kölcsönös támogatás, a kölcsönös támogatás és a képesség, hogy vezesse a kulturális vita a megfelelő matematikai nyelvet.
- emelni a felelősségérzet.
Felszerelés: poszterek, táblázatok, grafikonok, kártyák - lásd 1. függelék
Panel: tanár, szülő, diák.
Napirend (a konferencia terv):
- Üzenet 1. A történelem megoldására egyenletrendszerek / Ogloblina OS / Grade 9
- Adjon 2. megoldása rendszerek helyettesítésével / D. Khokhlov / Grade 9
- 3. Üzenet Systems szimmetrikus egyenletek / Troyanova K / 9 osztály
- 4. Adjon rendszerek lineáris egyenletek paramétereit / Zablocki AN / Grade 7
- Adjon 5. A geometriai megoldási módjainak egyenletrendszerek / VV Kravets / Grade 9
- 6. Adjon Cramer szabály vagy eljárás, meghatározói / Trifonov HU / 9 osztály
A kreatív munka - a kérdés a fal újság „Hírek a konferencia”
A történelem megoldására egyenletrendszerek.
Régóta kivétel az ismeretlen a lineáris egyenletek. A XVII - XVIII században kizárás kifejlesztett technikák Farm, Newton, Leibniz, Euler, Bézout, Lagrange (portrékat is látható az irodában).
A modern felvételi rendszer két lineáris egyenletek két ismeretlen a következő:
Az oldatot ez a rendszer által kifejezett képletek
Mivel a módszer koordináta létre a XVII században. Fermat és Descartes, lehetett megoldani rendszerek egyenletek grafikusan.
A Chaldean szövegeket III - II évezred Ez tartalmaz egy csomó problémát kell megoldani a segítségével elkészítése egyenletrendszer, amely magában foglalja az egyenleteket a másodfokú. Például feladat száma 20. tér a két négyzet tettem: 25. Oldalán a második oldalon a tér az első, és még mindig 5. A megfelelő rendszer egyenletek modern rekord:
helyettesítésével megkapjuk 1 x 2 + x = 6, megoldása az egyenlet, azt találjuk, x, akkor y.
Diophantosz, akinek nem volt elnevezések sok ismeretlen, nagy erőfeszítéseket tett, hogy kiválasszon egy ismeretlen módon, hogy csökkentsék a megoldást megoldása az egyenletrendszert.
Probléma 21. „Find két pozitív egész szám, tudva, hogy az összegük = 20, és a négyzetének összege a 208”.
A probléma megoldottnak az egyenletek a rendszer,
de Diofant megoldott kiválasztásával, mint a fele a különbség unknown unknown számokat, hogy
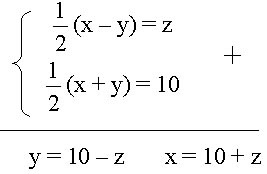
x 2 + y 2 = (Z + 10) 2 + (10 - Z) 2 = 2z + 2 200, és azzal a feltétellel, = 208
Z = ± 2 z = - 2- nem veri. körülmények között. feladatok
Azonban, ha Z = 2 x = 12 és y = 8.
Megoldás rendszerek a helyettesítési módszer.
Az egyenletrendszer találkoztunk során algebra 7. osztályban, de ez egy különleges fajta rendszer - a rendszer két lineáris egyenletek két változó
Az algoritmus, amely alakult a 7. osztályban, elég megoldására alkalmas rendszerek bármely két egyenlet két változó x és y.- Expressz szempontjából x egy egyenletrendszer.
- Behelyettesítve a kifejezés y a többi egyenlet a rendszer.
- Hogy oldja meg a kapott x = egyenletet.
- Helyettesítő váltakozva minden lépésben talált helyett a 3. gyöke x az expressziós y x, kapott az első lépésben.
- Record válasz formájában értékpárok (x; y).
Azt mutatják, hogy ez a módszer a problémák komplex rendszerek. / V. Kravets /
x 2 - xy - 2y 2 = 0
Mi megoldjuk a kapott egyenletet úgy, hogy x
A = y2 - 4 1 • (- 2y2) = 9u2. = 3 | y |
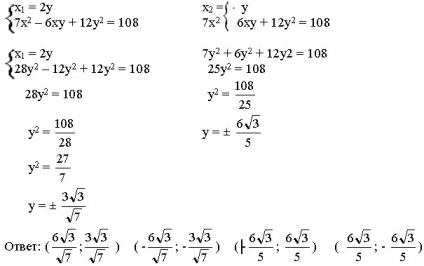
Megoldás szimmetrikus rendszerek egyenletek.
Van egy univerzális megoldás módszer: be helyettesítés
Mi átalakítani az első egyenletben a rendszer, hozzátéve, hogy mindkét fél a xy
x 2 + xy + xy + y 2 + xy = 4
2xy + x 2 + y 2 + xy = 4
Alkalmazzuk az egyetemes helyettesítés
Tekintsük a megoldás a másik rendszer

(X + y) 5 = x 5 + 5x 4 y + 10 x 3 y 2 + 10x 2 y 3 + 5xy 4 + y 5 = (x 5 + y 5) + 5xy (x 3 + y 3) + 10x 2 y 2 (x + y)
x 3 + y 3 = (x + y) 3 - 3HU (x + y), a következő képlet segítségével (2)
5 5 = 275 + 5Z • május 3 - 15z 2 • 5 + 10z 2 + 5 /. 25
Május 3 = 11 + 25z - 3Z 2 + 2z 2. Z 2 - 25z + 114 = 0
A rendszer lineáris egyenletek egy paramétert
Hadd emlékeztessem önöket a példák három eset lehetséges:
a) ha az együtthatókat X és Y nem arányos
b) amikor az arányoknak arányos
c) az együtthatók x arányos a együtthatója y, de nem áll arányban a szabad tagok.
Ez a tudás elengedhetetlen az alábbi feladatok megoldására:
* Határozza összes értékeit, amelyekre az egyenletrendszert

A geometriai módszer megoldására rendszerek egyenletek
Inverz tétele Pitagorasz-tétel, az x 2 + y 2 = 3 2. szám x és y jelentése a lábak ABD (D - vonal) a átfogója AB = 3.
Figyelembe véve a második egyenletet y 2 + z 2 = 16 konstrukciót BDC, ahol Y és Z - a lábak, és BC = 4 - átfogója.
A harmadik egyenlet y = XZ 2 azt sugallja, hogy a y arányos az átlagos szám x és z.
Az arányos szegmensek inverz tétel tétel abc = 90 0
AC = (x + z) = = 5,
Ezután AB 2 = AD • AC, 9 = x • 5 x =
BC 2 = DC • AC, 16 = z • 5, Z =
BD 2 = y 2 = x • z = ·
A módszer segítségével a veszteség gyökerei, könnyen elkészíthető,
hogy x = ± 9/5; y = ± 12/5; Z = ± 16/5.
Egy adott referencia rendszer lehet mások számára.
Például mi az értéke a kifejezés
xy + uz; x + y + z; x + y; x + z;
típusú rendszert nevezzük rendszer két lineáris egyenletek két ismeretlen, ahol a1; a2; B1; B2; C1 és C2 - számát. És a1 + c1 2 2 0 2 a2 + c2 2. 0.
Az egyik fő módszerek megoldására ez a rendszer az eljárás Kramer módszer vagy determinánsok. Az együtthatók ennek a rendszernek az a három meghatározó: (fő), X - X meghatározó ismeretlen; y - a meghatározó az ismeretlen y.
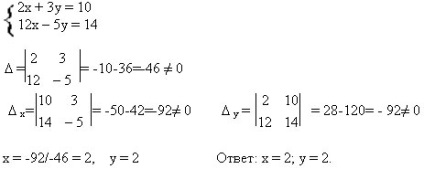
* Találd meg az összes értékeit paraméter b, amelyre a rendszer egy egyedi megoldás

A kreatív munka kártyák vzaimotrenazhera „Rajzolj koordinátákat.”
Oldja meg a rendszer, és létrejönne egy szám a koordinátákat.
A konferencia véget ért. Hiszem, hogy van egy vágy, hogy megpróbálja a kezét megoldására rendszereket. Vegye ki a munkát, és eljutni a kreatív munkát.
És most eljött az idő, hogy kiadja a következő kiadás a matematikai újság „Hírek a konferencián.”
1. GI Glaser, „A történelem, a matematika az iskolában”
2. IJ Depman „oldalanként algebra tankönyv”
3. ML Galitsky A.M.Goldman "problémák algebra 8-9"
4. AG Mordkovich "Algebra 9". "Algebra 7"
5. YN Makarychev "Algebra 9". "Algebra 7"