Lecke Focus - quadok
Jelek egy paralelogramma (dia 7)
Az ingatlan - a jele ennek az ellenkezője.
1) Ha a négyszög két szemközti oldalai párhuzamosak, és egyenlő, akkor a négyszög - paralelogramma.
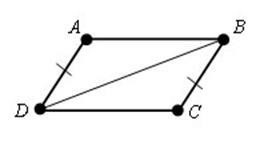
AD = BC, AD || BC, ABCD - paralelogramma
2) Ha a négyszög átlóival metszi és a metszéspont vannak osztva a felére, akkor ez a négyszög - paralelogramma.
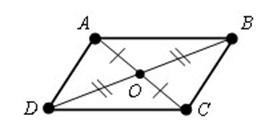
AB = OC
BO = OD, a ABCD - paralelogramma
3) Ha a négyszög szemközti szöge egyenlő, egy téglalap - egy paralelogramma.
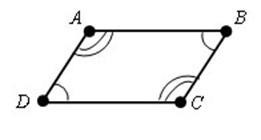
A = C
B = D, majd ABCD - paralelogramma
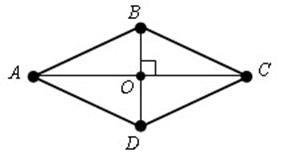
Definíció: Egy paralelogramma, amely minden oldalról egyforma.
1) vissza az összes tulajdonságait paralelogramma
2) átlói metszik a rombusz derékszögben. Átlói rombusz a szögfelezői szöge
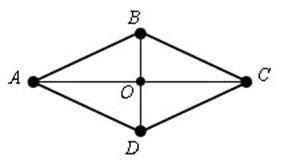
ABCD - a gyémánt, akkor; AC, DB - szögfelezői szögek
Ha az átlók paralelogramma merőlegesek, akkor a paralelogramma - egy gyémánt.
3. téglalap (diák 8-10)
Definíció: téglalapot nevezzük paralelogramma, amelyben az összes szög derékszög.
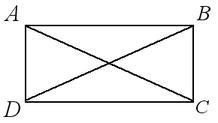
1) vissza az összes tulajdonságait paralelogramma
2) AVSDpryamougolnik átlója a téglalap ezután AC = BD.
A jel a téglalap: Ha a paralelogramma átlói egyenlő, akkor ez egy téglalap.
ABCD - egy paralelogramma; AC = BD ABCD - téglalap
Meghatározás: A tér - egy paralelogramma, amelyben az összes szög derékszög, és oldal egyenlő; téglalap, ha minden fél egyenlő; gyémánt, ahol a sarkokban - egyenes.
1) tulajdonságai a paralelogramma
2) Properties a téglalap
3) Tulajdonságok rombusz
5. Trapezoid (dia 15-17)
Definíció: Trapéz - egy négyszög, amelyben két oldalai párhuzamosak, és a két fél nem párhuzamosak. Párhuzamos oldalai nevezzük bázisok a trapéz (BC és AD.), A másik két - oldalfelületein (AB és CD).
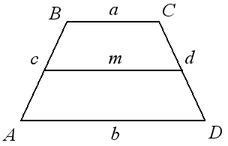
Egyenlő szárú trapéz, amelynek oldalai egyenlő AB = CD
1) A bázis szögek egyenlő:
2) Az átlók: CA = DB
Tünet: Ha a trapéz szögek a bázis egyenlő, akkor egyenlő szárú. Négyszögletes - a trapéz, amelyben az egyik szög 90 °.
III. Feladatok (dia 18-43)
1. Az ABCD paralelogramma. Szög A jelentése 30 °. Keresse meg a szögek egy paralelogramma.
2. kerülete paralelogramma egyenlő 200 cm. Az egyik oldal 25 cm. Keresse meg a többi oldala a paralelogramma.
3. Az ABCD paralelogramma AB oldal 10 cm. Az átlós AC és BD pontban metszik egymást. O, és egyenlő a 14 cm és 10 cm. Megtalálja a határoló a háromszög AOB.
4. Problémák a választott válasz
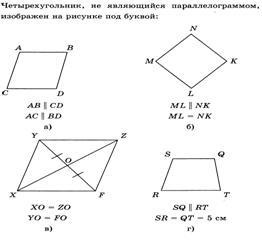

5. A ABCD négyszög BC = AD és AD || Sun, BAC + ACD = 80 o. Megtalálja, amit ezek mindegyike az szögek.
6. Az ABCD BA = CD és AB || DC, CBD = 15 o. Mi az a szög VDA?
7. paralelogramma KMNP hajtjuk szögfelező MKP, MN irányban, amely metszi pontban E. Keresse paralelogramma oldalán KR KMNP ha NE = 8 cm, és a kerülete a paralelogramma 40 cm.
1. A kerülete a téglalap 28 cm, és annak egyik oldalán, legalább egy másik 4cm. Ezután a kisebb oldalon egyenlő?
2. Az egyik sarokban a négyszög által alkotott átlók egyenlő 120 °. Kisebb a téglalap 8 cm. Keresse az átlós a téglalap.
3. A ABCD téglalap átlósan persekayutsya át O. ACD = 60 o. BD = 10 cm. Keresse meg a CD-oldalon.
4. A ABCD téglalap átlós leállítjuk a ponton O. BAC = 50 o. Pont - a középső AB. Mekkora szöget zár be az EOD.
5. A probléma a választás a válasz:

1. Problémák a választott válasz:
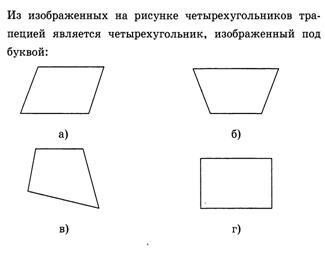



2. A trapéz MNKL átlós MK KL, NMK = KML = 30 °. A kerülete a trapéz egyenlő 30 cm. Find NK.
3. A téglalap alakú trapéz hegyesszög 45 °. A kisebb az oldalsó és a kisebb bázis egyenlő 10 cm. Find nagyobbik alapja.
1. A gyémánt ABCD szög egyenlő 31 °. Diagonals metszik a pont O. Keresse meg a háromszög szögei BOC.
2. rombusz ABCD Mintegy - a metszéspontja az átlók, E és F felezőpontja BC és a DC. Bizonyítsuk be, hogy EF = BO EF és az AC.
3. rombusz ABCD Mintegy - a metszéspontja az átlók, OM, OK, OE - merőlegesek csökkent az AB, BC, CD volt. Bizonyítsuk be, hogy OM = OK. Keresse meg a szögek összege egyetértési és CDE.
4. Keresse meg a rombusz szögei, ha egyik szöge 70 °.
5. A cukorka ABCD oldalsó 5 cm, AVD szög 60 ° és átlós kerülete Analyzed BD.
1. Az ábrán ABCD - egy téglalap. Bizonyítsuk be, hogy a négyszög egy négyzet az ICPD.
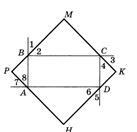
2. Az ABC háromszög B = 90 o. AB = BC. Az oldalon AB és BC vett pontokat M és R. Az AC oldalán - pontok K és H, úgy, hogy a négyszög mRNS - egy négyzet. MR = a cm. Keresse AC.
3. Az ábra ABCD - téren. AK = PD = EC = BM. Bizonyítsuk be, hogy a Merck - egy négyzet.
1. Textbook Geometry fokozat 7-9, ed. Atanasyan LS
2. Ziv BG "Oktatási anyagok Geometry" Grade 8
3. munkafüzet a geometria Atanasyan LS
4. AV Farkov "Vizsgálatok Geometry" Grade 8