Khí-négyzet eloszlás
Vegyünk egy khí-négyzet eloszlás. A MS EXCELHI2.RASP () függvény konstruáljuk grafikonok az eloszlási függvény és a valószínűség-sűrűség, magyarázni a használatát, ezen értékesítési a matematikai statisztika.
Chi négyzet (X2 HI2, angl.Chi-squareddistribution) használják a különböző módszerek a matematikai statisztika:
Definíció. Ha x1. x2. ..., xn független valószínűségi változók által forgalmazott standard normális eloszlás N (0, 1), az eloszlása a véletlen változó Y = x 1 2 + x 2 2 + ... + X n 2 X 2 egy eloszlású n szabadsági fokkal.
RaspredelenieH 2 függ egy paramétert, az úgynevezett szabadsági fok (df, degreesoffreedom). Például, az építőiparban konfidenciaintervallumai becslések variancia számával megegyező szabadsági fokok df = n-1, ahol n - a minta mérete.
A sűrűség eloszlása által kifejezett általános képletű 2:
grafikonok funkciók
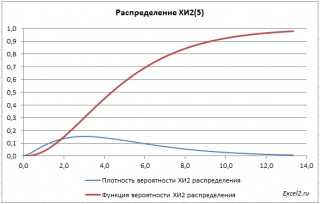
A fájl a lapon példa Graph ábrán grafikonok valószínűségi eloszlást, kumulatív eloszlás függvénye.
Hasznos ingatlan HI2-eloszlás
Let x1. x2. ..., xn független valószínűségi változók, normális eloszlású μ azonos paraméterek és σ, míg XCR számtani átlaga ezen értékek x.
Aztán a véletlen változó y
2-nek egy X-eloszlású n-1 szabadsági fokkal. Használata a meghatározása a fenti minta diszperziót expresszió lehet újraírni az alábbiak szerint:
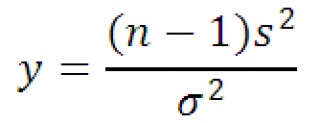
Következésképpen a szelektív forgalmazás statisztikák y, a mintavétel során a normál eloszlás. X2 eloszlású n-1 szabadsági fokkal.
Ez a tulajdonság szükségünk lesz az építési megbízhatósági intervallumok értékelésekor szóródása a forgalmazás. mert diszperziós csak akkor lehet pozitív szám, és X 2 forgalmazást alkalmaznak az értékeléséhez, majd dB y> 0, meghatározott definíciójában.
HI2-eloszlás MS Excel
Megjegyzés. mert HI2-eloszlás speciális esete a gamma eloszlás. GAMMA.RASP képlet = (x; n / 2, 2, TRUE) n pozitív egész szám visszaadja ugyanazt az eredményt, mint a képletben = HI2.RASP (x; N; IGAZ) vagy = 1 HI2.RASP.PH ( x, n). GAMMA.RASP képletű A = (x; n / 2; 2; HAMIS) visszaadja ugyanazt az eredményt, mint a képletben = HI2.RASP (x; N; HAMIS). azaz veroyatnostiHI2 eloszlást.
HI2.RASP.PH () függvény az eloszlásfüggvény. pontosabban - jobb valószínűsége, azaz P. Egyértelmű, hogy az egyenlőség
HI2.RASP.PH = (x; n) + HI2.RASP (x; n; IGAZ) = 1
mert Az első ciklus kiszámítja a valószínűsége P, és a második P.
HI2.RASP () az egyetlen funkció, amely visszaadja a sűrűségfüggvénye HI2-eloszlás (a harmadik érvet kell állítani FALSE). A többi funkció vissza a eloszlásfüggvény. azaz a valószínűsége, hogy egy valószínűségi változó értékét veszi fel a megadott tartomány: P.
A fenti funkciók vannak megadva MS EXCEL fájlba például a munkalapon funkciók.
Mi annak a valószínűsége, hogy az X valószínűségi változó értéket vesz fel kisebb vagy egyenlő, mint egy adott x. P. Ez történhet több funkciója van:
HI2.RASP = (x; n; IGAZ)
= 1-HI2.RASP.PH (x; n)
= 1-HI2RASP (x; n)
HI2.RASP.PH () függvény a valószínűsége P, az úgynevezett jobb valószínűsége tehát, hogy megtalálják P, meg kell kivonni 1 az eredmény.
Nézzük mi annak a valószínűsége, hogy az X valószínűségi változó értéket vesz fel nagyobb egy adott x. P. Ez történhet több funkciója van:
= 1-HI2.RASP (x; n; IGAZ)
HI2.RASP.PH = (x; n)
HI2RASP = (x; n)
Az inverz függvény HI2-eloszlás
Az inverz függvény kiszámítására használjuk az alfa kvantilis. azaz számítástechnikai értékek x adott valószínűségi alfa. ahol x kell elégítenie az expressziós P = alfa.
HI2.OBR () függvény kiszámítására használják konfidenciatartományát szórása normális eloszlást.
HI2.OBR.PH () függvény kiszámítására használjuk a felső ötöd. azaz Ha az argumentum a függvény megadott szignifikancia szinten, például 0,05, a függvény egy értéke az X valószínűségi változó úgy, hogy a P = 0,05. Mivel egy összehasonlító függvényt HI2.OBR () értéket ad vissza az X valószínűségi változó úgy, hogy a P = 0,05.
A fenti funkciók felcserélhető, mint Az alábbi képletek vissza ugyanazt az eredményt:
= HI.OBR (alfa; n)
HI2.OBR.PH = (1-alfa; n)
HI2OBR = (1- alfa; n)
Néhány példa a számítások vannak megadva a példa fájl a munkalapra funkciókat.
MS Excel függvények használatával HI2-eloszlás
A vonatkozó magyar és angol funkció nevek:
HI2.RASP.PH () - Eng. Íme CHISQ.DIST.RT, azaz Khí-négyzet eloszlás jobb hátsó, jobb farkú Chi-négyzet (d) forgalmazási
HI2.OBR () - Eng. Íme CHISQ.INV, azaz Khí-négyzet eloszlás inverz
HI2.PH.OBR () - Eng. Íme CHISQ.INV.RT, azaz Khí-négyzet eloszlás inverz Jobb hátsó
HI2RASP () - Eng. CHIDIST név, funkció megegyezik CHISQ.DIST.RT
HI2OBR () - Eng. Íme CHIINV, azaz Khí-négyzet eloszlás inverz
Becslése eloszlás paraméterek
mert Általában HI2 forgalmazás céljára felhasznált matematikai statisztika (a számítás konfidenciaintervallumok hipotézis vizsgálatára stb), és szinte soha nem készíthet modelleket a valós értékek allokáció ezt a vitát a becslések az eloszlás paraméterei nem kerül végrehajtásra.
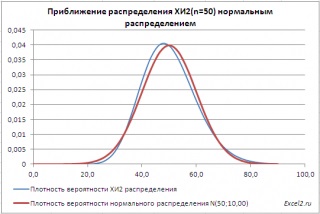
Közelítő HI2-eloszlás a normális eloszlás
Ha a szám a szabadsági fokok n> 2 X 30 eloszlás jól közelíthető normális eloszlású μ = n és a variancia σ = 2 * n (lásd. Példa közelítése kép lap).