Keresse meg az előírt értéket
Keresse meg a megadott határértékeket:
a) Behelyettesítve a változó annak határérték 2 kapjunk
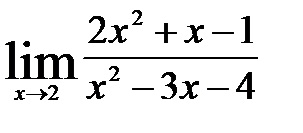
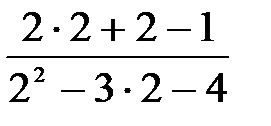
b) Behelyettesítve ez a változó határérték -1 kapunk meghatározatlan formában.
A ártalmatlanítása ilyen típusú bizonytalansági ebben az esetben képviseli a másodfokú polinom a számláló és a nevező, mint a termék lineáris szorzók segítségével az ismert képlet:
ahol - a gyökerek a másodfokú polinom
.
Mi. a diszkrimináns másodfokú polinom
Most, egy példa a feltétel lehet újraírni eltérő formában, és kiterjeszti az oldatot:
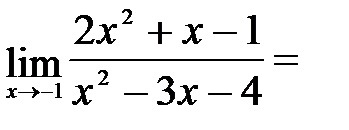
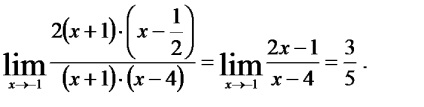
Itt állunk szemben bizonytalanságot. amely lehet megszabadulni a kiszabott zárójelben a számláló és a nevező a legmagasabb fokozatot, vagy előre változó számlálóját és nevezőjét a frakció osztva. n, ahol a legmagasabb fokú a számláló és a nevező.
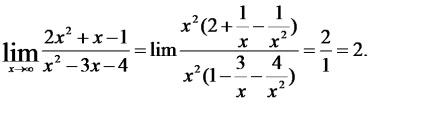
Az első esetben a mentességet bizonytalanság fogjuk használni az első figyelemreméltó limit és az egyik nyilvánvaló következménye van:
Példák Az oldatok a következő lesz:
A második esetben a mentességet bizonytalanság fogjuk használni a második figyelemreméltó limit és az egyik nyilvánvaló következménye van:
Példák Az oldatok a következő lesz:
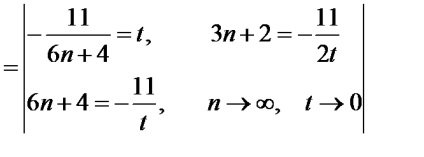
Közvetlen helyettesítése a határérték az érvelés eredménye egyfajta bizonytalanság. , Szorozzuk meg a számláló és a nevező az a frakció, hogy felfedje ezt az összeget a bizonytalanság
Keresse származékok. a szabályok és képletek a differenciálás. A címzés összes alábbi példák mellett a táblázatban jól ismert szabályai differenciálódás mennyiségű származékokat használunk, akkor a különbség, a termék, lövés, és a tétel a származék egy összetett függvény.
g) Ha olyan összetett függvény, ahol ez, ha az egyes funkciók és különbséget illetően az állítása, majd
Annak vizsgálatára, a funkció a módszerek differenciálszámítás felhívni a grafikonok. A tanulmány a funkciók és a grafikus ajánlott az alábbiak szerint:
1) Határozza meg a domain a funkció
2) Annak vizsgálatára funkcióját folytonosságát; talál egy pontot diszkontinuitás a funkció és a határok egyoldalú pontokon diszkontinuitás;
3) megtalálják a szélsőérték pont funkció, és meghatározni a monotonitás időközönként;
4) megtalálja az inflexiós pont a grafikonon, és határozzuk meg időközönként konvexitás és konkáv a grafikon;
5) Keresse meg a aszimptotáját a grafikonon;
6) felhívni egy grafikon, a korábbi vizsgálatok eredményét;
7) a funkciót találni a legnagyobb és a legkisebb érték az intervallumban
1) A tartomány ennek a funkciónak minden valós érték az az érv, hogy az, =. ami azt jelenti, hogy a függvény folytonos az egész számegyenesen és grafikon nincs függőleges asymptote.
2) tanulmányozza a funkció a szélsőérték és időközönként monotonitás. Ebből a célból, azt látjuk, annak származéka, és nullának:
. Megoldása a másodfokú egyenlet kapott, arra a következtetésre jutunk, hogy a függvénynek két kritikus pont 1 sort: Osszuk a domain Ezeknek a pontoknak a részek és származékok változtatni a bejelentkezési őket felfedi időszakok monotónia és a jelenléte a szélsőséges.
3) határozza meg az inflexiós pont a grafikon, a szünetekben való konvexitás és konkáv. Ahhoz, hogy megtalálja a második deriváltja az adott funkciót, és állítsa nullára:
; .
Ez a függvény az egyik kritikus pont 2 fajta
Osztjuk a domain a kapott pont az a része, amelyek mindegyike meghatározza a jele a második derivált:
Az érték az abszcissza a inflexiós pont a gráf függvénnyel, és az ordináta e pont:
4) Határozzuk meg a jelenlétét a grafikon egy adott funkció lejtőn a aszimptotával. Ahhoz, hogy határozza meg a paramétereket az egyenlet aszimptóta használatra képletek:
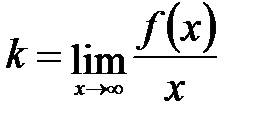
Így, a grafikon az adott funkció nem ferde aszimptotákkal.
5) a telek választott koordinátarendszerben képviseli a maximális pontot. minimum. inflexiós és grafikák metszéspontja tengely
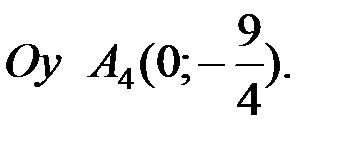
Figyelembe véve a korábbi vizsgálatok eredményét konstrukció a görbe.
6) megkeressük a legnagyobb és a legkisebb érték az adott funkció az intervallum szám értékeket ezt a funkciót végein ebben a szegmensben, a kritikus pontok egyféle fogott a szegmensben, és hasonlítsa össze az eredményeket:
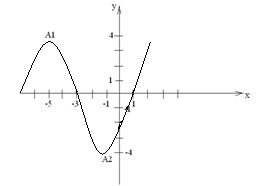
Fedezze fel a következő függvény, és létrejönne egy sematikus ábra:
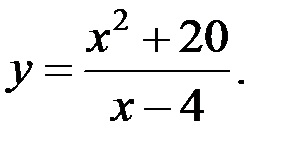
1) terület meghatározására:
2) Tanulmány a folyamatosság és diszkontinuitás pont besorolás.
Mivel függvény folytonos mindenhol, kivéve a ponton. Kiszámítjuk az egyoldalú határértékek ezen a ponton:
Így egy adott pont ez a funkciója a második fajta a töréspontot, és a vonal grafikon függőleges asymptote.
3) Tanulmány a szélsőérték és monotónia időközönként.