Irracionális egyenletek köbös gyökök
Téma: „Az irracionális egyenlet formájában. . "
Irracionális egyenletek egyenletek, ahol a variábilis található jel alatt a gyökér (radikális) vagy jelentkezzen emelése frakcionált teljesítmény.
Az egyenlet a f (x) = g (x), ahol legalább az egyik a kifejezést f (x) vagy g (x) irracionális irracionális egyenlet.
Alapvető tulajdonságai gyökök:
- Minden gyökök még fokú aritmetikai, azaz ha a radicand negatív, akkor a radikális nincs értelme (nem létezik); ha a radicand nulla, a radikális is egyenlő nulla; ha a radicand pozitív, akkor van egy radikális és pozitív értéket.
- Minden gyökök páratlan fokú meghatározható bármilyen értéke radicand. Ebben az esetben, a radikális negatív, ha a radicand negatív; nulla, ha a radicand nulla; pozitív, ha a meghódított pozitív.
Megoldási módjait, irracionális egyenletek
Problémák irracionális egyenlet - ez azt jelenti, hogy megtalálja az összes érvényes változó érték, amely, ha helyette az eredeti egyenlet, ez lesz a valódi numerikus egyenlőség, illetve annak bizonyítására, hogy ezek az értékek nem léteznek. Irracionális egyenletek megoldani a valós számok halmaza R.
Tűréstartománya az egyenlet áll ezeket az értékeket a változó, amelyben az összes nem-negatív kifejezése mellett a radikális jele még diplomát.
A fő megoldási módjainak irracionális egyenletek:
a) az építési mód mindkét részének az egyenlet azonos mértékben;
b) eljárás olyan új változók (módszer változások);
c) Lehetséges megoldások megoldására irracionális egyenletek.
Ez a cikk középpontjában a vizsgálata a fenti egyenletekben egy bizonyos típusú és így 6 megoldási módjait, az ilyen egyenletek.
Ez a módszer a szorzás és rövidített képlet nem tartalmazza a „víz alatti” köveket, azaz Ez nem vezet a kialakulásához idegen gyökereit.
Átírjuk az egyenlet formájában egy kocka, és vozvedom mindkét oldalon. Kapunk egy egyenletet egyenértékűek az adott egyenlet
2. példa: oldja egyenletet.
Átírjuk az egyenlet formájában egy kocka, és vozvedom mindkét oldalon. Kapunk egy egyenletet egyenértékűek az adott egyenlet
és megvizsgálja a kapott egyenlet a négyzetgyöke relatív
így, a diszkrimináns 0, és az egyenlet lehet egy oldat X = -2.
Megjegyzés. Az ellenőrzést elhagyható abban az esetben doreshivaetsya másodfokú egyenlet.
2 módszer. Cubed formula.
Továbbra is épít az egyenlet a kocka, de a használata módosított készítmények rövidített szorzás.
(Enyhe módosításával az ismert képletek), majd a
3. példa. Oldjuk meg az egyenletet.
Vozvedom harmadfokú egyenlet használatával a fenti képletek.
Mindazonáltal, az egyenlőnek kell lennie a jobb oldalon. Ezért van:
Most kockázott megkapjuk a szokásos másodfokú egyenlet:
, és két gyökereihez
Mindkét érték, amint azt a csekket, helyes.
De nem az összes átalakítás egyenértékű? E kérdés megválaszolása előtt, nézzük megoldani egy egyenletet.
Example4. Oldjuk meg az egyenletet.
A figyelem, mint korábban, mindkét része a harmadik fokozat, van:
Hely (adott ez a kifejezés zárójelben ugyanaz), megkapjuk:
. Mi jussanak és ellenőrizzék .Sdelaem x = 0 -postoronny gyökér.
Választ a kérdésre: „Miért van külföldi gyökerei?”
Egyenlőség azt jelenti, egyenlőséget. Csere c, megkapjuk:
Ez könnyen azonosságának igazolására
Tehát, ha az egyik vagy. Az egyenlet felírható formájában.
Cserélésével c, azt látjuk, hogy ha egyik vagy
Ezért, amikor ezt a módszert az oldatot feltétlenül kell tennie egy átvilágítás, és győződjön meg arról, hogy nem vittünk gyökereit.
3. módszer. rendszer módszer.
5. példa megoldásához egyenletet.
Bemutatjuk a csere, összetételét, és megoldani a egyenletrendszert.
amennyiben nyilvánvaló, hogy
A második egyenletet kapjuk úgy, hogy egy lineáris kombinációja kifejezések a gyökök nem függ az eredeti változó.
Ez könnyen elkészíthető. hogy a rendszerben nincsenek megoldások, és így az eredeti egyenletnek nincs megoldás.
Válasz. Nem gyökereit.
6. példa megoldásához egyenletet.
Bemutatjuk a csere, összetételét, és megoldani a egyenletrendszert.
Visszatérve az eredeti változó, van:
4 módszer. Egy monoton függvény.
Mielőtt ezt a módszert használja, hogy kapcsolja elmélet.
Meg kell a következő tulajdonságokkal:
- Ha a függvény az y = f (x) és y = g (x) növeli (csökkenti) egy sor, akkor a függvény az y = f (x) + g (x) is növeli (csökkenti) a készletben.
- Ha a függvény az y = f (x) és y = g (x) növeli (csökkenti) egy sor, abban, amit mind figyelembe nemnegatív értékeket minden elfogadható x, az y = f (x) g (X) növekszik (csökken ) egy adott készlet.
- Ha a függvény az y = f (x) egy monoton, az egyenlet f (x) = a nem több mint egy megoldást.
- Ha a függvény az y = f (x) és y = g (x) különböző jellegű monotonitási, az egyenlet f (x) = g (x) nem több, mint egy megoldást.
- típusú funkció növeli a k> 0, és csökken a K<0.
7. példa megoldásához egyenletet.
A bal oldalon az egyenlet növekvő függvénye, és a jobb oldalon - ez a szám, azaz állandó, ezért az egyenletnek legfeljebb egy gyökér, amely kiválasztja az x = 9. Győződjön meg arról, hogy a gyökér alkalmas.
8. példa megoldásához egyenletet.
A bal oldalon az egyenlet növekvő függvénye, és a jobb oldalon - ez a szám, azaz állandó értékű, ezért az egyenletnek legfeljebb egy gyökér, amely kiválasztja: x = -2. Győződjön meg arról, hogy a gyökér alkalmas.
Az utóbbi egyenlet képviseli más formában, majd a jobb oldalon az egyenlet csökken, míg a bal oldali növekszik, így az egyenletnek legfeljebb egy gyökér. és érkeznek x = -2.
5 módszer. Grafikus módszer egyenletek megoldására.
9. példa egyenlet megoldásához
Átírjuk az egyenlet: konstrukció grafikonokat a bal és jobb oldalán.
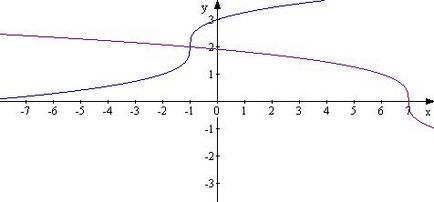
A grafikonok metszik a pont (1; 2), X = -1.
Ellenőrzés: 2 = 2 (jobbra).
X = - 1 a gyökere az eredeti egyenlet.
6 módszer. helyettesítő módszer
Példa. Oldjuk meg az egyenletet:
Bemutatjuk a csere. Hagyja, akkor az egyenlet
t = 0, vagy - nincsenek megoldásokat.
t = 0, akkor visszatér az eredeti változó, van: x = -8.
Feladatok a független döntést.