Integrálása racionális frakciók - studopediya
Meghatározás: Elemi frakciókat úgynevezett a következő négy típus:
m, n - egész számok (m ł 2, n ³ 2) és a b 2 - 4ac <0.
Az első két típusú integrálok elemi frakciók meglehetősen egyszerű táblázat helyettesítésével t = ax + b.
Tekintsünk egy módszert integráló elemi frakciókat a III forma.
III beépített típus frakciót fejezhető ki:
Ott látható általános formában leadott szerves III típusú frakciókat két táblázatos integrálok.
Tekintsük a kérelmet a fenti képlet a példákban.
Általánosságban elmondható, hogy ha a trinomiális ax 2 + bx + c expressziós b 2 - 4ac> 0, akkor a frakció definíció szerint nem egy egységet, de mindazonáltal lehetséges, hogy integrálja a fenti módszerrel.
Mi most úgy a módszere az integráció részleges frakciók IV típusú.
Először is, úgy a speciális esetben, ahol M = 0, N = 1.
Ezután a beépített típus érhető szelekció tökéletes négyzet nevező képviseletében a. Azt, hogy a következő átváltási:
A második integrál ebben az egyenletben, megtesszük darabonként.
Az eredeti szerves kapjuk:
Az így kapott képlet nevezzük megismétlődik. Ha alkalmazza azt az n-1-szer, megkapjuk a standard integrál.
Mi most visszatérünk az integrál az elemi frakciók a IV forma általában.
Az első integrál egyenlet történő helyettesítésével kapott
2 + s kap az asztalra. megismétlődik képlet érvényes a fentiekben tárgyalt A második integrál.
Annak ellenére, hogy a látszólagos összetettsége az integráció a IV típusú elemi frakciók, a gyakorlatban, ez elég könnyű használni frakciók egy kis mértékben n. és az egyetemes és egységesen járjanak lehetővé teszi egy nagyon egyszerű megvalósítása ennek az eljárásnak a számítógépen.
Annak érdekében, hogy integrálja a racionális frakció szükséges bontja elemi frakciók.
Tétel: Ha - megfelelő racionális frakció, a nevező P (x) képviseli, mint a termék lineáris és másodfokú tényezők (megjegyezzük, hogy minden polinom valós együtthatók lehet az ebben a nyomtatványban: P (x) = (X - a) egy ... (x - b) b (x 2 + px + q) l ... (x 2 + RX + s) m), akkor ez a frakció lehet bontani elemi szerint a következő séma szerint:
Az integráció a racionális frakciók igénybe az eredeti bomlás elemi frakciók. Ahhoz, hogy megtalálja az értékek Ai. Bi. Mi. Ni. Ri. Si használják úgynevezett eljárás meghatározatlan együtthatók. amelynek lényege abban a tényben rejlik, hogy két polinom azonosan egyenlő, szükséges és elegendő ahhoz, hogy egyenlő a együtthatóit, mint hatásköre x.
Az E módszer alkalmazása tekintsünk egy konkrét példát.
Ami a közös nevező, és egyenlővé megfelelő számláló, megkapjuk:
mert lövés rossz, meg kell először izolálni az egész része:
Felbontjuk a nevező a kapott frakciók faktorizáció. Látható, hogy amikor X = 3, a nevező nulla lesz. majd:
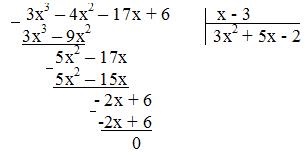
Így 3x 3 - 4x 2 - 17x + 6 = (X - 3) (3x 2 + 5x - 2) = (X - 3) (x + 2) (3x - 1). majd:
Annak elkerülése érdekében, meghatározatlan, ha a zárójelben nyilvánosságra együtthatók, csoportosítás, és megoldások a rendszer (ami meglehetősen magas néhány esetben) használunk módszerrel úgynevezett önkényes értékek. A módszer abban áll, az a tény, hogy az expressziós fentiekben levezetett szubsztituált váltakozva több (számának megfelelően meghatározatlan együtthatók) tetszőleges x értékei. Az egyszerűség kedvéért a számításokat vett önkényes értékek figyelembe a pontot, ahol a nevező a frakció nulla, azaz a a mi esetünkben - 3, -2, 1/3. kapjuk: