Hatékony módszerek megoldására konkrét és megfelelő integrálok

Home | Rólunk | visszacsatolás
Ez a rész további anyagokat megoldási módjait, konkrét és megfelelő integrálok. Feltételezzük, hogy az olvasó egy közepes vagy nagy integrációs képességek. Ha nem, kérjük kezdeni az alapokat: a határozatlan integrál, példák megoldásokat.
Amennyiben a határozatlan integrál - van közel és határozott integrál. A Newton-Leibniz formula, akkor is meg kell ismernie első kézből. Továbbá, a probléma megoldására a számítástechnika a négyzetes planáris alakú (lásd. 7.2.3.) És a számítás a forgástest mennyiség (cm. 7.2.4.).
A lecke célja azoknak, akik szeretnék megtanulni, hogyan lehet megoldani a határozott és a helytelen integrálok gyorsabban és hatékonyabban. Először is, úgy a funkciók integrálása páros és páratlan függvény egy szimmetrikus intervallum nulla körül. Akkor fogunk foglalkozni a probléma megtalálni a terület a kör a határozott integrál. Ez a cél az is fontos, hogy bemutatja, hogy a közös technika integrálása határozott integrál - trigonometrikus cserélni. Soha nem látott - az új cucc!
Hasonlóképpen, úgy a nem megfelelő integrálok páros és páratlan funkciók a szimmetrikus intervallumot. Különösen, több ritka típusú helytelen integrálok, amelyek nem szerepelnek az alapanyagban az előző részekben, amikor az alsó határt általában „mínusz végtelen”, amikor mind a határértékek a végtelenbe, ha mindkét végét az intervallum integrációs funkció szenved végtelenített rés (ez egy szerves a második fajta). És ez egy ritka helytelen integrál - egy pont a diszkontinuitás intervallumban az integráció.
Egy megoldási módja a határozott integrál egy még függvény szimmetrikus nullára szegmens
Tekintsük a határozott integrál az űrlap
Ez könnyű észrevenni, hogy az intervallum integráció [-c; c] szimmetrikus tekintetében nulla.
Ha az integrandust f (x) páros. akkor az integrál
Ez számítható a fele a szegmens, és az eredmény - kettős:
Sok kitalálta, hogy miért van ez így, de vegyük egy konkrét példát a rajz:
Számoljuk ki a határozott integrál
Mintegy paritás funkció sok minden elhangzott a módszeres anyag grafikonok és tulajdonságait elemi függvények. Még egyszer: egy páros függvény, ha az egyenlőség f (-x) = f (x) neki.
Hogyan lehet ellenőrizni a funkció paritás? Meg kell vmestox helyettesítheti -x.
Ebben az esetben: és.
Tehát, ez a funkció még.
A szabály szerint, hogy szimmetrikus nulla körüli intervallumban [-2; 2], a mi integrálja egy még funkció a következőképpen számítható ki:
Most, geometriai értelmezést. Igen, továbbra is kínozzák a szerencsétlen parabola ....
Bármilyen chotnaya funkció különösen. szimmetrikus tengely OY:
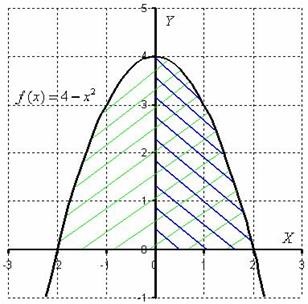
számszerűen egyenlő a terület síkidom, amely árnyalt zöld. De, mivel a paritás az integrandus, és ebből következően a szimmetria a menetrend a tengelyhez képest OY. elegendő ahhoz, hogy területének kiszámítására a szám, árnyékos kék, és az eredmény - megduplázódott. Azonos félből egy geometriai expressziós tulajdonságai paritás. Ezért az igazi hatás
Egy hasonló történet előfordul bármilyen páros függvény f (x) intervallumban szimmetrikus nulla:
Egyesek azt mondják: „De mindez miért van szükség, mert tudja, és így kiszámítani a határozott integrál.” Lehetséges. Nézzük számítani:
De attól, hogy kényelmes volt, hogy helyettesítse a negatív alsó határ? Nem nagyon. By the way, egy nem nulla százalékos diákok hibázik a jeleket. Sokkal könnyebb és élvezetesebb helyettesítő nulla. Megjegyzendő, hogy ez még mindig egy egyszerű demo, a gyakorlatban minden rosszabb.
Továbbá vétel jelentési gyakran kiszámításához használt kettős integrálok. tripla integrálok. ahol a számítástechnika és annyira hiányzik.
Rövid példa a független megoldások:
Számoljuk ki a határozott integrál
Teljes körű megoldásokat és válaszokat a végén a leckét.
Felhívjuk figyelmét, hogy ha felkérik, hogy kiszámítja a határozott integrál, a rajz nem szükséges! Az 1. ábra például csak azért, hogy ez egyértelmű szabályt. Csak ezúttal szentelt a következő egyszerű feladat:
3.1. Számoljuk ki a határozott integrál
3.2. Területének kiszámítására síkidom vonallal körülhatárolt
. és OX tengely időközönként.
Ez két különböző probléma! Először is nézzük foglalkozik az első pont:
1) Az integrandus még az integráció intervallum szimmetrikus nulla, így:
Határozott integrál negatív lett, és ez történik!
Most azt látjuk, a terület síkidom. Itt nélkül próbáltak kezelni nehéz:
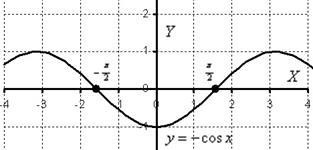
A grafikonon a szegmens található tengely alatti OX. ezért:
A terület nem lehet negatív, ezért a képlet hozzáadjuk mínusz a terület számítása (lásd. Még a 3. példát a 7.2.3.).
Megjegyezzük, hogy a koszinusz paritás nem törölték, így ismét osztva az intervallumot és megduplázódott integrál.