Geometriai értelmében a származék - studopediya
A származékot és a differenciál
Tegyük fel, hogy a függvény az y = f (x) meghatározott intervallumon X. Vegyünk egy pontot
x Î H. Adjunk egy növekménye értéke x Dx ¹ 0, akkor a függvény kap a növekmény D y = f (x + Ax) - f (x).
A függvény deriváltját y = f (x) nevezzük határa az arány a növekmény funkció a növekmény az érvelés, amikor az utóbbi nullához (ha ez a határérték létezik).
A származék is nevezzük Y „és dy / dx.
Geometriai értelmében a származék
Ahhoz, hogy megértsük a geometriai jelentése a származék, úgy a problémát az érintő.
Tekintsünk egy sík grafikon egy folytonos függvény az y = f (x) (lásd. 3.1 ábra).
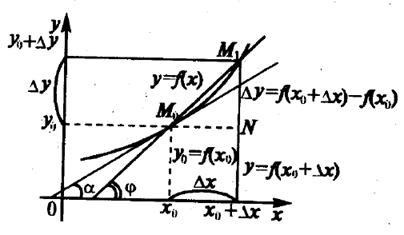
Készítünk egy érintőleges ez a görbe a ponton a M0 (x0. Y0). Először meg kell határozni a fogalmát érintőjének. Ehhez az érv adunk egy növekménye x0 Dx, és adja át a görbe y = f (x) egy pontot
M0 (x0. F (x0)), hogy a pont az M1 (X0 + Ax, F (X0 + Ax)). Rajzolj egy kereszteződés M0 M1. Az érintő a görbe y = f (x) megvalósítani a végállás a szelő közelítés M0 M1 M1 egy pont-pont M0. azaz amikor Dh®0.
Corner vágási M0 M1 faktor (tangense dőlésszöge e j vonal a abszcissza) megtalálható a DM0 M1 N :. Ezután a lejtőn a tangens (szög tangense a) egyenlő.
Így a származék a függvény meredeksége az érintő a grafikon az X-tengelyen (tangenciális szögletes együttható).