Galilei-transzformáció

7. fejezet Speciális tárgyak (privát) relativitáselmélet

Ha egy referenciakeret mozgó egymáshoz képest egyenletesen és egy egyenes vonal, és ezek közül az egyik igaz törvényeket a newtoni dinamika, ezek a rendszerek tehetetlenségi. Azt is megállapították, hogy mind a tehetetlenségi vonatkoztatási rendszerek jogszabályok klasszikus dinamika azonos alakúak; Ez sutmehanicheskogo relativitás elve (elve galileai relativitás).

Ennek bizonyítására, nézzük két referencia képkocka: inerciális rendszer K (a koordinátái x, y, z), amelyet szokványosán rögzítettnek feltételezzük, és a rendszer a K „(koordinátákkal x”, y „z”), mozgó képest egységes egyenes vonalú sebességgel (= const). A visszaszámlálás indul, amikor az eredete a két rendszer megegyezik. Tegyük fel, hogy egy tetszőleges időben t elrendezése e rendszerek egymáshoz képest már a bemutatott formában ris.58. Sebesség irányul mentén 00 „a sugár vektor a O O”.

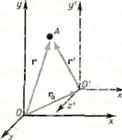
Találunk közötti összefüggést koordinátáit egy tetszőleges pontjában mindkét rendszeren. Tól ris.58 látható, hogy

Egyenlet (34,1) lehet írva nyúlványok a koordinátatengelyeken:

Egyenleteket (34,1) és (34.2) nevezzük Galilei koordináta transzformációk.

Abban a speciális esetben, amikor a K „mozog mentén a sebességet pozitív iránya az X tengely mentén K. rendszer (a kezdeti időben tengelyek egybeesnek), Galileo átalakítása koordinátákat van formájában

A klasszikus mechanika, azt feltételezzük, hogy az idő múlása nem függ a relatív mozgás vonatkoztatási rendszerek, vagyis arra, hogy az átalakulás (34.2), akkor adjunk hozzá még egy egyenlet ..:

Felvett kapcsolatok csak akkor érvényesek, abban az esetben a klasszikus mechanika (), illetve a sebesség összehasonlítható a fény sebessége, a Galileo átalakulás helyett a sokkal általánosabb transzformációk Lorentz (H.Lorents (1853-1928) - holland fizikus) (§36).

Differenciálás kifejezés (34,1) időalapú (figyelembe véve (34,3)), megkapjuk az egyenlet

amely soboypravilo sebesség mellett a klasszikus mechanika.

A gyorsulás a referencia-képkocka K

Így, a gyorsulás a pont a referencia képkockák K és K”, mozgó egymáshoz képest egyenletesen és egyenes vonalban ugyanazon:

Következésképpen, ha az A pont a másik test nem érvényes (= 0), akkor szerint a (34,5), n = 0, m. E. rendszer R „jelentése egy inerciális (pont mozog ahhoz képest egyenletesen és egyenes vonalúan vagy nyugalmi).

Így, egyenletből (34,5) a következőképpen bizonyítéka mechanikai relativitás elve: egyenlet dinamikájának az átmenet az egyik inerciális referencia rendszer egy másik nem változott, azaz yavlyayutsyainvariantnymi tekintetében koordináta-transzformációk ... Galileo jegyezni, hogy bármilyen mechanikus kísérletek, végzett a Inerciarendszer, lehetetlen megállapítani, hogy ez nyugalomban vagy mozgó egyenletesen egy egyenes vonal. Például ül a kabinban a hajó mozog egyenletesen egy egyenes vonal, nem tudjuk meghatározni a hajó pihen, vagy mozog, nem nézett ki az ablakon.