Fizikai alkalmazások sor integrálok
Dolgozz azáltal, hogy a test egy erőtér;
A mágneses mező körül a karmester egy áram (Amper törvény);
Elektromágneses indukció egy zárt hurokban a mágneses fluxus (Faraday-törvény).
Úgy véljük, ezek részletesebben alkalmazási példákat.
Tegyük fel, hogy egy darab huzalt ismertet térbeli görbe, \ (C \) Legyen a masszát oszlik el ez a görbe sűrűségben \ (\ rho \ bal (\ jobbra). \), Akkor a teljes súlya a görbe által kifejezett egy vonalintegrál az első fajta \ [m = \ int \ limits_C \ right) ds>. \] Ha a görbe \ (C \) van meghatározva, amely paraméteres formában egy vektorral függvény \ (\ mathbf \ bal (t \ right) = \ left (\ jobbra), \) akkor a tömege által leírt \ [m = \ right) \ sqrt >>> \ right)> ^ 2> + >>> \ right)> ^ 2> + >>> \ right)> ^ 2 >> dt>.> \ ] esetében egy sík görbe által meghatározott sík \ (Oxy, \) úgy definiáljuk, mint a tömeg \ [m = \ int \ limits_C \ right) DS> \] vagy parametrikusan th formában \ [m = \ right) \ sqrt >>> \ right)> ^ 2> + >>> \ right)> ^ 2 >> dt>.> \]
A tömegközéppontja és tehetetlenségi nyomatékok a görbe
Ismét hagyja, hogy egy darab huzalt ismertet görbe \ (C, \) és a tömegeloszlás a görbe mentén meghatározott sűrűségű folytonos függvény \ (\ rho \ bal (\ jobbra). \) Ezután, a koordinátákat a központ a meghatározott képleteket görbe tömegeket \ [\ bar x = \ frac >>>, \; \; \ bar y = \ frac >>>, \; \; \ bar z = \ frac >>>, \] ahol \ [> = \ int \ limits_C \ right) ds>,> \; \;> = \ int \ limits_C \ right) ds>> \; \;> = \ int \ limits_C \ right) ds >> \] - az úgynevezett elsőrendű pillanatokat.
A tehetetlenségi nyomatékok tengelyek \ (Ox, Oy \) és \ (Oz \) határozza meg \ [= \ int \ limits_C +> \ right) \ rho \ bal (\ right) ds>,> \; \; = \ Int \ limits_C +> \ right) \ rho \ bal (\ right) ds>,> \; \; = \ Int \ limits_C +> \ right) \ rho \ bal (\ right) ds>.> \]
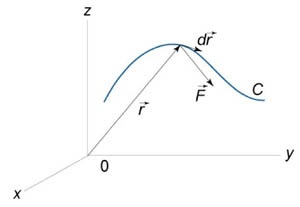
Munka mozgatásával a test egy erőtér \ (\ mathbf \) a görbe mentén \ (C \) expresszálódik egy vonalintegrál a második fajta \ [W = \ int \ limits_C \ cdot d \ mathbf>, \] ahol \ (\ mathbf \) - ható erő a test, \ (d \ mathbf \) - a készülék érintő vektor (ábra \ (1 \)). Symbol \ (\ cdot d \ mathbf> \) jelöli a skaláris szorzata vektorok \ (\ mathbf \) és \ (d \ mathbf. \)
Vegye figyelembe, hogy erőtér \ (\ mathbf \) nem feltétlenül okozza a test mozgását. A test képes mozgatni hatása alatt más erők. Ebben az esetben, a munkaerő \ (\ mathbf \) néha negatív.
Ha a vektor mező értéke a koordináta formájában egy \ [\ mathbf = \ left (\ jobbra), Q \ left (\ jobbra), R \ left (\ jobbra)> \ jobbra), \] területén munkát képlettel számítottuk ki \ [W = \ int \ limits_C \ cdot d \ mathbf> = \ int \ limits_C. \] a konkrét esetben, amikor a test mentén mozgó lapos görbe \ (C \) a síkban \ (Oxy, \), a képlet \ [W = \ int \ limits_C \ cdot d \ mathbf> = \ int \ limits_C, \] ahol \ (\ mathbf = \ left (\ jobbra), Q \ left (\ jobbra)> \ jobbra). \)Ha a vektor mező \ (\ mathbf \) lehetséges. a működését a test mozgás az \ (A \) azon a ponton, \ (B \) által expresszált \ [W = u \ left (B \ right) - u \ left (A \ jobbra), \] ahol \ (u \ bal (\ right) \) - potenciál a területen.
Testtömeg \ (m \) van kiöntve szögben a horizonton \ (\ alpha \) kezdeti sebességgel \ (\) (ábra \ (6 \)). Számoljuk ki a munka vonzóerő \ (\ mathbf = m \ mathbf \) mozgása során a test akár az ütközés pillanatában a földre.
Írunk a törvény a mozgás a test egy paraméteres formában. \ [X => t = \ cos \ alpha \ cdot t, \] \ [y => t - \ frac >> = \ sin \ alpha \ cdot t -. \ Frac >> \] Upon ütközés a talajjal \ ( y = 0, \) úgy, hogy a repülési idő a test egyenlő \ [\ sin \ alpha \ cdot t - \ frac >> = 0> \; \; \ Sin \ alpha - \ frac >> \ right) = 0,> \; \; \ Sin \ alpha >>.> \] A gravitációs erő felírható \ (\ mathbf = m \ mathbf = m \ left (\ jobbra). \), Akkor a munka a mozgás a test egyenlő \ [>> + Q \ frac> >> \ right) dt >> = \ sin \ alpha >> \ normalsize >>> - g \ cdot \ frac >>> \ right) dt >> = <- g\int\limits_0^\sin\alpha>> \ Normalsize >>>> \ right) dt = >> <- g\int\limits_0^\sin\alpha>> \ Normalsize >> = <- g\left[ \right|_^\sin\alpha>> \ Normalsize >> \ right]> = <- g\left[ \sin \alpha \cdot t - \frac>>> \ right)> \ right | _ ^ \ sin \ alpha >> \ normalsize >> \ right]> = <- g\left( ^2>\ Alpha >> - \ frac ^ 2> \ alpha >>>>> \ right) = 0.> \] Ezt az eredményt azzal a ténnyel magyarázható, hogy a gravitációs mezőben a Föld a lehetséges, mivel a egyenlőség \ [\ frac >> = \ frac >> = 0. \] Megkeressük a potenciál ezen a területen. Általánosságban, úgy azt a \ [\ right) = \ int + \ left (y \ right)> = + \ left (y \ right)> = + \ left (y \ jobbra).> \] Feltételezve, \ (\ nagy \ frac >> \ normalsize = Q \ left (\ right) = - g, \) találj \ [\ frac> \ left (y \ right) = - g, \; \; \ Rightarrow \ bal (y \ right) = - Gy + \] Tehát, a gravitációs mező potenciál egyenlő \ [u \ left (\ right) = -. Gy + = C -. Gy \], ahol \ (C \) - állandó, amelyet be lehet állítani egyenlő \ (0 \) az eredmény egy potenciális \ [u \ left (\ right) = -. Gy \] Ez azt mutatja, hogy amikor a test elmozdul a kiindulási pont \ (O \ balra (\ jobbra) \) a végpontig \ (a \ bal (\ right) \) munka egyenlő \ [W = u \ balra (a \ right) - u \ left (O \ right) = 0. \]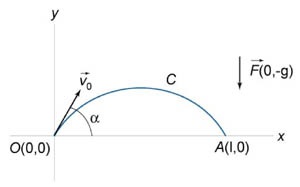
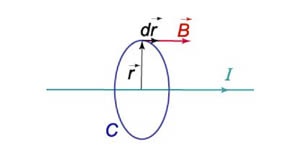
Számítsuk ki a mágneses indukció vákuumban távolságban \ (r \) a tengelynek egy végtelen hosszú áramvezető \ (I. \)
Ahhoz, hogy megtalálja a mágneses mező rasstonii \ (r \) a vezető, úgy kör alakú kontúr sugara \ (r, \) merőlegesen helyezkedik el; az áramvezető (ábra \ (7 \)). Mivel a mező \ (\ mathbf \) irányul érintőlegesen a kör alakú kontúr bármely ponton, a skalár szorzata vektorok \ (\ mathbf \) és \ (d \ mathbf \) egyszerűen \ (BDR. \) Akkor tudjuk írni \ [ \ OINT \ limits_C \ cdot d \ mathbf> = \ OINT \ limits_C = B \ OINT \ limits_C = 2 \ pi rB \] Az eredmény egy \ [2 \ pi rb = I \ ;. \; \ szöveg \; \; B = \ fracI >>>. \]
Becsült értéke elektromotoros erő \ (\ varepsilon \), és az elektromos mező \ (E, \) felmerülő gyűrű méretét \ (1 \, \ text \) a repülőgép utas, ha a légi jármű repülési mágneses mező sebességgel a Föld \ (900 \, \ szöveget. \)
Szerint a Faraday-törvény \ [\ varepsilon = \ OINT \ limits_C = -. \ Frac >> \] Mivel a vezető gyűrűt mozog a Föld mágneses mezeje, termel változás mágneses fluxus \ (\ psi, \) áthaladó a gyűrű.
Tegyük fel, hogy a mágneses mező \ (\ mathbf \) síkjára merőleges a gyűrű. Majd a \ (\ Delta t \) áramlás változása egyenlő \ [\ Delta \ psi = 2rBx = 2rBv \ Delta t, \] ahol \ (x = v \ Delta t, \) \ (v \) - repülőgép sebessége, \ (B \) - a mágneses mező a Föld. Az utolsó kifejezést kapjuk \ [\ varepsilon = - \ frac >> = 2rBv \.] Behelyettesítve a megadott értékeket \ [v = 900 \, \ text = 250 \, \ text \; \ r = 1 \, \ text = 0,01 \, \ text \; \ B = 5 \ alkalommal> \, \ text \] megtalálják az értéket az EMF \ [\ Varepsilon = 2rBv = 2 \ cdot 0,01 \ cdot 5 \ alkalommal> \ cdot 250 = 0,00025 \, \ szöveget. \] Amint látható, ez elég biztonságos az utasok számára.
Feszültség felmerül elektromos mező határozza meg képlet \ (\ varepsilon = \ int \ limits_C \ cdot d \ mathbf>. \) Szimmetria, az indukált elektromos mező lesz egy konstans amplitúdójú bármely pontján a gyűrű. Ez irányul érintőlegesen a gyűrű bármely pontján. Ez megkönnyíti, hogy kiszámítja a vonalintegrál. \ [\ Varepsilon = \ OINT \ limits_C \ cdot d \ mathbf> = \ OINT \ limits_C = E \ OINT \ limits_C = 2 \ pi rE. \] Következésképpen, az elektromos térerősség egyenlő \ [E = \ frac> = \ frac >> = 0004 \, \ szöveget. \]