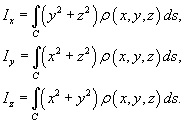Geometriai és fizikai alkalmazások kettős, hármas, görbe vonalú és felületi integrál -
2. Fizikai alkalmazások integrálok
kettős integrálok 2.1Fizicheskie alkalmazások
A tömeg és nyomatékok a statikus lemezek
Tegyük fel, hogy a sík lemez készül inhomogén anyag, és elfoglalja az R régióban az Oxy síkban. Legyen a sűrűsége a lemez egy ponton (x, y) az R egyenlő. Ezután a tömeg a lemez keresztül expresszáljuk kettős integrál formájában
Statikus nyomaték lemez relatív Ox tengely határozza meg a képlet
Hasonlóképpen a statikus pillanat a lemez tengelyéhez képest Oy.
A koordináták a tömegközéppontja a lemez. foglalja el a régió R a síkon Oxy sűrűséggel elosztott a törvény szerint által leírt képletek

Egy homogén lemez sűrűsége az összes (x, y) az R tömegközéppontja esetben csak a forma és a területet nevezzük súlypontja.
A tehetetlenségi nyomatéka a lemez
A tehetetlenségi nyomaték a lemez tengelyéhez képest Ox képlete
Hasonlóképpen számítjuk tehetetlenségi nyomaték lemez tengelyéhez képest Oy.
Polar tehetetlenségi nyomatéka a lemez
Tegyük fel, hogy az elektromos töltés eloszlik az R régióban az Oxy síkban és annak eloszlása sűrűség függvény kap. Ezután a teljes díjat adják plastinyQ
A középérték függvény
Itt is a képlet dyal kiszámítják az átlagértéket az elosztott értékeket. Legyen f (x, y) egy folytonos függvény a zárt R régióban az Oxy síkban. Mean értéke μ f (x, y) által meghatározott területen az R
ahol - a terület az integrációs térség R.
Számítsuk ki a tehetetlenségi nyomatéka a háromszög egyenes vonalak határolják, (2. ábra), és amelynek sűrűsége.
Megtaláljuk a tehetetlenségi nyomaték a lemez tengelyéhez viszonyítva Ox.

Hasonlóképpen, kiszámítjuk a tehetetlenségi nyomaték a tengely körül Oy.
2.2 Fizikai alkalmazások triple integrálok
A tömeg és a statikus pillanatok a test
Legyen a test foglal térfogatban U és ömlesztett sűrűsége az M pont (x, y, z) van megadva a függvény ρ (x, y, z). Ezután telam tömeg kerül kiszámításra a hármas integrál:
A statikus pillanatok a test relatív a koordinátarendszerhez képest síkban Oxy, Oxz, Oyz által kifejezett képletek
Koordinátáit a súlypont adja meg:
Ha a test egyenletes sűrűségű ρ (x, y, z) = 1 M pont (x, y, z) a U. súlypontja geometriájától függ a test és az úgynevezett centroid.
Tehetetlenségi nyomatéka
A tehetetlenségi nyomatékok koordinátarendszerben Oxy, Oxz, Oyz által adott
és tehetetlenségi pillanatok tengelyek körül Ox, Oy, Oz vannak képletek alapján számítandó
Mint látható, a kapcsolatok
A tehetetlenségi nyomaték a testet a származási integrál
Tehetetlenségi nyomaték tekintetében a származási lehet kifejezni a tehetetlenségi nyomaték tekintetében a koordináta síkok:
Ez tenzor szimmetrikus, és ezért lehet csökkenteni, hogy átlós formában egy bizonyos választott tengelyek Ox „Oy”, Oz”. Az értékek a átlós elemek (redukció után a diagonális formája tenzor) nevezzük a fő tehetetlenségi nyomatékok. és az említett irány - sajátvektorok vagy fő tengelye tehetetlenség.
Ha egy test forgási tengelye körül nem sovpadayushey a főtengelye a tehetetlenség, akkor tapasztalni rezgés a magas fordulatszámon. Ezért amikor ilyen eszközök kialakításának az szükséges, hogy a forgástengely egybeesik az egyik fő tengelye tehetetlenség. Például, ha egy gumiabroncs-kiegyensúlyozó azok pótlásával történik: a kis súly adunk a kereket, hogy egy meccset a forgástengelye a fő tengely tehetetlenségi és meg kell szüntetni a rezgést.
A gravitációs potenciál és a gravitációs erő
Newtoni test potenciál a P pont (x, y, z) jelentése az integrál
ahol ρ (ξ, η, ζ) - sűrűsége a test és a.
Az integrációs végezzük a hangerő-a test. Ismerve a potenciális lehet kiszámítani gravitációs anyagi pont m tömegű, a test és elosztott előre meghatározott sűrűségű ρ (ξ, η, ζ), amelyet a képlet
ahol G - a gravitációs állandó.
Find gömb sugara R. tömegsűrűsége γ arányos a távolság négyzetével a központtól.
A hipotézis, a sűrűség arányú γ beállítva γ = ar 2., ahol egy - egy állandó, R - a távolság a központtól. A tömeg a labda kényelmes számítani a gömbi koordináták:

2.3 Fizikai alkalmazások vonal integrálok
A görbe vonalú integrálok számított
A tömegközéppontja és tehetetlenségi nyomatékok a görbe;
Dolgozz azáltal, hogy a test egy erőtér;
A mágneses mező körül a karmester egy áram (Amper törvény);
Elektromágneses indukció egy zárt hurokban a mágneses fluxus (Faraday-törvény).
Úgy véljük, ezek részletesebben alkalmazási példákat.
Tegyük fel, hogy egy darab huzalt ismertet térbeli görbe, C. Tegyük fel, hogy a tömeges eloszlik a görbe mentén a sűrűség ρ (x, y, z). Ezután a teljes tömege a görbe által kifejezett egy vonalintegrál az első fajta
Ha a görbe C paraméteres formában adtuk egy vektorral funkciót, tömege által leírt képlet
Abban az esetben, egy sík görbe meghatározott Oxy síkban. Ez a tömeg szerinti
vagy paraméteres alakban
A tömegközéppontja és tehetetlenségi nyomatékok a görbe
Ismét hagyja, hogy egy darab huzalt által leírt egy C görbe, és a tömegeloszlás mentén egy folytonos görbét meghatározott sűrűség függvény ρ (x, y, z). Ezután a koordinátáit a tömegközéppontja a görbe által meghatározott képletek
- az úgynevezett elsőrendű pillanatokat.
A tehetetlenségi nyomatékot a tengelyek Ox, Oy és Oz által meghatározott