Építőipari háromdimenziós figurák GeoGebrában 3d
GeoGebra - egy ingyenes, cross-platform dinamikus matematikai program az oktatás minden szintjén, beleértve a geometria, algebra, táblázatok, grafikonok, statisztikák és számtani, egy egyszerűen használható csomagban.
Ezen túlmenően a program gazdag lehetőségeit dolgozó funkciók (grafikus, számítási gyökerek, szélsőérték, integrál, stb), mivel a beépített parancs nyelv (ami mellesleg lehetővé teszi, hogy kezelni és geometriai szerkezetek).
Más programokkal ellentétben dinamikus manipuláció a geometriai objektumok jön az ötlet GeoGebra egy interaktív kombinációja geometriai, algebrai és számreprezentációs. Hozhat létre tervez a pontok, vektorok, vonalak, kúpszeletek valamint a matematikai függvények, majd dinamikusan megváltoztatni őket.
Továbbá GeoGebra lehetővé teszi, hogy közvetlenül meg koordinátákat egyenlet és manipulált. Így könnyen lehet, hogy grafikonok funkciók működnek csúszkák kiválasztására szükséges paramétereket kíván szimbolikus származékai és használata erős parancsokat, mint Root és a következetesség.
GeoGebra program interfész (GeoGebra) hasonlít egy táblára, amelyen felhívni grafikonok, geometriai formák jöjjenek létre, stb A program ablak jelenik meg egyértelműen a változtatások, ha megváltoztatja az egyenletet, akkor a görbe rekonstruálható változtatni a mérleget vagy térbeli helyzetét, az egyenlet van írva mellett a görbe akkor automatikusan igazodik az új értékeket.
GeoGebra program széles körben használják a felhasználók millióinak szerte a világon, hogy tanítani algebra és geometria. A tanulási folyamat vizuális köszönhetően a vizuális formában használja az alkalmazást.
Jellemzők a matematika nem korlátozódnak az építési ütemterv, GeoGebra program használható interaktív rajzok megoldására geometriai problémákat. GeoGebra program hatékony és funkcionalitást, amely lehetővé teszi, hogy világosan és egyszerűen tanulni a matematikát.
A kérelem tartalmazza a geometria, algebra, lehetséges aritmetikai műveletek végrehajtását, ami táblázatok, diagramok, működés lehetséges a statisztikát, működjön együtt a funkciókat támogatja az animáció létrehozását, stb A GeoGebra programmal lehet létrehozni a különböző 2D és 3D alakzatok, interaktív videókat, amit aztán le lehet helyezni az interneten.
Minden alkalmazás, amelyek részét képezik a GeoGebra program áll rendelkezésre, és szinkronban vannak egymással dolgozni, mint a csomag részét képezi.
GeoGebra készítette Marcus Hohenvarterom. A program Java nyelven íródott, az alkalmazás támogatja a különböző operációs rendszerek: Windows, Mac OS X, Linux, Android.
A gyártó honlapján lehet letölteni a rendszeres változata a program telepítéséhez GeoGebra a számítógépen. Is, akkor töltse le a hordozható változat (GeoGebra Portable) a megfelelő operációs rendszer.
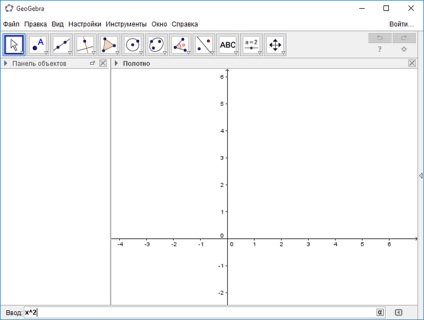
Elindítása után GeoGebra a számítógépen, megnézzük a program interfész.
Menüsoron. meg lehet változtatni a beállításokat a program a menüből.
Eszköztár. Vannak eszközök objektumok létrehozásához. Kattintás után a háromszög a jobb alsó sarokban a gomb megnyitja további eszközöket. Műveletek elérhető az eszköztár segítségével végezhető el a beviteli sor.
Object panel. Az objektumok panel tartalmazza a bemeneti változók és függvények. Ehelyett a változó nevek jelennek meg itt az értéküket. Látni, hogy a formula szimbolikus formában, akkor kell kattintani a jobb egérgombbal.
Gomb „Undo” és „Újra”.
A bemeneti vonal. Ez a fő eszköz dolgozik a programban GeoGebra. Itt kiadni a parancsokat és a tápszerek adott változók értékeit. A jobb „Team List” beviteli sorban van egy gomb. A további parancsokat is megadhat parancsokat és szimbólumokat a billentyűzeten.
Munkaterületet. Minden konstrukciók a programban készül a munkaterületen. Akkor nagyítás az egér kerék, mozogni a munkaterület koordinátatengellyel.

Ezután próbálja végezni néhány alapvető műveletet a programban GeoGebra.
Rajzoló funkciókat GeoGebrában
Megépíteni a függvény grafikonját elég lesz, hogy írja be a mezőbe. Jelenítse meg a parabola kell írni a vonal „Enter” a következő kifejezés:
A „*” jelet a programban GeoGebra jelöli hatványozást.
Ezután kattintson az «Enter» gombot. Ezt követően a menetrend épül a munkaterületen. A minta lehet méretezni az egér használata. Mozgatni a munkaterületet kell kattintani a gombra «Shift», miközben lenyomva tartja a bal egérgombot.
Tudod mozgatni a chart önmagában le a jobb egérgombot, miközben az Objektumok részen megjeleníti a változásokat az egyenletben.

Létrehozása háromszög GeoGebrában
Próbáljuk felhívni a háromszög GeoGebra programot. Ehhez be kell menni a „geometriai” módban, hogy bekapcsolja a rács, és tiltsa le a kijelző Koordinátatengelyek.
Kattintson a jobb gombbal a koordinátatengelyeken, a helyi menüben válasszuk a „Grid”, majd ott kattintson az elem „Tengely” letiltása koordinátatengelyeken. Az eszköztáron kattintson a „Polygon”.
A húzás után egy háromszög, egymás beállításával három csúcsa. Ha szükséges, akkor adja meg a pontos koordinátákat. Ehhez meg kell kattintani a ponton, a jobb gombbal.

Ezután létrehozhat egy felezővonal a szög. Ehhez kattintson a háromszög gomb gomb alatt „merőleges vonal” és válassza ki a szerszám „kettéosztott sarok” a legördülő listából. Ezután kattintson képező szögfelező jön létre két szegmens.
A program elérhető online változata GeoGebra: Geogebra Online (GeoGebra Online). A rendszerváltást követően az www.geogebra.org oldalon. meg tudja nyitni a programot GeoGebra a böngésző, hogy végre a szükséges intézkedéseket. Így még telepítése nélkül GeoGebra program a számítógépen, ha az internet, akkor a munka ezen a matematikai program bejelentkezik az online szolgáltatást a mobil eszközön.


Mivel az építkezés a legegyszerűbb geometriai alakzatok között tárgyalt az előző fejezetben, amikor leírja a szerszámok, akkor nem kell venni ebben a fejezetben. Ez a fejezet egy workshop a fejlesztési GeoGebra környezet (3DwithJOGL2) példákon keresztül konkrét feladatokat. Feladatok úgy választjuk, hogy teljes mértékben fedezze a lehetséges geometriai szerkezetek segítségével GeoGebra közegben (3DwithJOGL2).
Kiválasztása prizma funkciót, és vegye figyelembe az 5. pont a koordináta tengelyen a 15. ábrán látható.
Megnyomja a z-tengely a kívánt magasságba, megkapjuk a prizma ABCDEA1B1C1D1E1. (16. ábra)