elemi transzformációs eljárás (Gauss-Jordan gauss és felkutatására, az inverz mátrixok)
Az első rész tartották a módszert találni az inverz mátrix keresztül cofactors. Itt leírjuk egy módszert találni inverz mátrixok Gauss elimináció átalakulások és a Gauss-Jordan. Gyakran előfordul, hogy ez a módszer a megállapítás a fordított mátrix módszer az úgynevezett elemi transzformációk.
Módszer elemi transzformációk
A módszer használatához egyetlen mátrixban rögzített, előre meghatározott mátrix $ A $ azonosító mátrix, és $ E $, azaz mátrixát alkotják formájában $ (A | E) $ (ezt a mátrixot is nevezik kiterjesztett). Ezt követően, a segítségével elemi transzformációk végzett húrok kiegészített mátrix azt érjük el, hogy a mátrix bal jellemzője lesz egy, a kibővített mátrix formájában $ \ left (E | A ^ \ right) $. Elemi transzformációk ebben a helyzetben ezeket a műveleteket:
- Változás két üléssor.
- Szorzás az összes sorok számos nem egyenlő nullával.
- Az elemeken kívül a egyik sor megfelelő elemeivel egy másik sorban szorozva olyan tényezőt.
Alkalmazza az elemi transzformációk különböző módon. Általában a kiválasztott Gauss vagy Gauss-Jordan eliminációs módszerrel. Általában a módszerek Gauss és Gauss-Jordan célja, hogy megoldja rendszerek lineáris algebrai egyenletek, nem megtalálására fordított mátrixok. A „alkalmazása minánsok, hogy megtalálják a visszacsatolás mátrix” itt úgy kell érteni, hogy „a kérelem műveletek módszerben rejlő Gauss, megtalálására fordított mátrixba.”
Számozás példák folytassa az első rész. A példákban tárgyalt №5 és №6 használja minánsok, hogy megtalálják a fordított mátrixhoz, mint a példákban №7 és №8 felhasználásával szintaktikusán elemezzük módszer Gauss-Jordan. Megjegyezzük, hogy ha során az oldatokat minden elemét egy sorban vagy oszlopban a mátrix van elrendezve, hogy jellemzői nullázni, a fordított mátrix nem létezik.
Keresse meg a mátrix $ A ^ $, ha $ A = \ left (\ begin 7 4 6 \\ 2 5 -4 \\ 1 -1 3 \ end \ right) $.
Ez a példa található inverz Gauss-módszerrel. Bővített mátrix, amelynek a formája $ (A | E) $, ebben a példában formájáról: $ \ left (\ begin 7 4 6 1 0 0 \\ 2 5 -4 0 1 0 \\ 1 -1 3 0 0 1 \ end \ right) $.
A cél: elemi transzformációk okoznak hatalmas mátrix formában $ \ left (E | A ^ \ right) $. Mi ugyanezt a lépést, hogy a használt megoldására rendszerek lineáris egyenletek a Gauss. Alkalmazásának Gauss módszer akkor hasznos, ha az első elem az első sor expandált mátrix egységet. Ahhoz, hogy ezt elérjük, felcserélni az első és a harmadik sorban a kiegészített mátrix, amely lehet: $ \ left (\ begin 1 -1 3 0 0 1 \\ 2 5 -4 0 1 0 \\ 7 4 6 1 0 0 \ end \ right) $.
Most folytassa a döntést. Gauss van két szakaszra oszlik: az előre stroke és a visszatérő (részletes leírást a módszer megoldására egyenletrendszer megadott a megfelelő szálak példákat). E két lépést kell alkalmazni a folyamat találni a fordított mátrixba.
egyenes irány
A nulla ki elemei az első sorban az első oszlop, alatt található az első sorban:

Hasonlóképpen, a művelet végrehajtása és a $ III-7 \ cdot I $. Ha nehézségei vannak az ezek megvalósítását műveletek, azok külön-külön végezzük (hasonlóan a fent bemutatott akció $ II-2 \ cdot I $), és az eredmény, akkor ahhoz, hogy a kibővített mátrix.
A második sorban a második oszlop zeroize tagja alatt elhelyezett második sor:
Osszuk a harmadik sorban 5:
Előre elgázolta. Minden elem alatt a fő diagonális mátrix, hogy a jellemzőit, nulla.
megfordítás
A nulla ki elemeket a harmadik sor harmadik oszlop felett található a harmadik sorban:
Mielőtt a következő lépés részben a második sor $ 7 $:
A nulla ki elemeit a második sor második oszlop felett elhelyezett második sor:
Az átalakítás befejeződött, a fordított mátrix a Gauss módszer talált: $ A ^ = \ left (\ kezdődik -11/5 18/5 46/5 \\ 2 -3 -8 7/5 \\ -11/5 -27/5 \ end \ right) $. Ellenőrizze, szükség esetén lehet ugyanaz, mint az előző példákban. Ha kihagyja a magyarázatok, a megoldás formájában:

Válasz. $ A ^ = \ left (\ begin -11/5 18/5 46/5 \\ 2 -3 -8 7/5 \\ -11/5 -27/5 \ end \ right) $.
Keresse meg a mátrix $ A ^ $, ha $ A = \ left (\ begin -5 4 1 0 \\ 2 3 -2 1 \\ 0 7 -4 -3 \\ 1 4 0 6 \ end \ right) $.
egyenes irány

Átalakítása előre menetben befejeződött. Minden elem alatt a fő diagonális mátrix bal oldalán a funkciók, reset.
megfordítás

A fordított mátrix a Gauss módszer található, $ A ^ = \ left (\ kezdődik -13/14 -75/8 31/8 7/2 -19/8 \\ -117/16 49/16 11/4 -23/4 \\ -141/8 57/8 \\ 13/2 17/8 103/6 -43/16 -9/4 \ end \ right) $. Ellenőrizze, szükség esetén elvégzi ugyanúgy, mint a példákban №2 és №3.
Válasz. $ A ^ = \ left (\ begin -13/14 -75/8 31/8 7/2 -19/8 \\ -117/16 49/16 11/4 -23/4 \\ -141/8 57/8 \\ 13/2 17/8 103/6 -43/16 -9/4 \ end \ right) $.
Keresse meg a mátrix $ A ^ $, ha $ A = \ left (\ begin 2 3 4 \\ 7 1 9 \\ -4 5 -2 \ end \ right) $.
Ahhoz, hogy megtalálja az inverz mátrix művelet alkalmazható tipikus módszer Gauss-Jordan elimináció. Ellentétben Gauss bemutatott módszer az előző példákban №5 és №6. Azt, hogy a döntés végezzük egyetlen lépésben. Hadd emlékeztessem önöket, hogy a Gauss módszer két részre oszlik: az előremenetben ( „csinál” nulla alatt a fő diagonális mátrix, hogy a vonal) és a fordított (nulla ki az elemeket a fő diagonális mátrix a sorban). Kiszámításához a fordított mátrixba a Gauss-Jordan eljárás két megoldás nem szükséges lépéseket. Először is kiterjesztett tömböt: $ (A | E) $:
$$ (A | E) = \ left (\ begin 2 3 4 1 0 0 \\ 7 1 9 0 1 \\ 0 -4 5 -2 0 0 1 \ end \ right) $$
Állítsa vissza az összes bejegyzés az első oszlopban, hanem egy. Az első oszlopban, minden elem nulla, tehát lehet választani elemet. Vegyük például a $ (- 4) $:
A kiválasztott elem $ (- 4) $ van a harmadik sorban, ezért a harmadik sorban is használni, hogy állítsa vissza a kijelölt elemeket az első oszlopban:
Legyen az első eleme a harmadik sorban lett egyenlő eggyel. Ehhez osszuk el a harmadik sorban a kiegészített mátrix elemei $ (- 4) $:
Most folytassa alaphelyzetbe a megfelelő elemeket az első oszlop:
A további lépéseket kell használni a harmadik sorban lesz már lehetetlen, mert már használják az első lépés.
Úgy döntünk, egy nem nulla eleme a második oszlop, és nullázza ki az összes többi elemét a második oszlopban. Mi lehet választani bármelyik két elem: $ \ frac $ vagy $ \ frac $. Eleme $ \ left (- \ frac \ right) $ nem lehet kiválasztani, mert ez található a harmadik sorban, amit használnak, az előző lépésben. Válasszon egy elemet $ \ $ frac található, amely az első sorban. Legyen úgy, hogy ahelyett, hogy $ \ $ frac az első sorban volt az egység:
Most, nullázza a megfelelő elemek a második oszlop:
Az ezt követő vitában az első sorban nem lehet használni.
Be kell állítani az összes elemét a harmadik oszlop, egyet kivéve. Meg kell választani egy nullától eleme a harmadik oszlop. Azonban nem tudunk $ \ frac $ vagy $ \ $ frac, mivel ezek az elemek vannak elhelyezve az első és harmadik sor, amit használnak. A választás korlátozott: továbbra is csak egy eleme $ \ $ frac található, amely a második sorban. Osztjuk az összes elemet a második sorban a $ \ frac $:
Most, nullázza vonatkozó elemeit a harmadik oszlop:
Átalakítás módszerével Gauss-Jordan befejeződött. Továbbra is csak azért, hogy a mátrix vonások válni egységet. Ehhez meg kell változtatni a sorrendjét a sorok. Kezdetként felcserélni az első és harmadik sor:
$$ \ left (\ begin 1 0 0 47/4 -13/2 -23/4 \\ 0 0 1 -39/4 11/2 19/4 \\ 0 1 0 11/2 -3 -5/2 \ end \ right) $$
Most cserélni a második és harmadik sor:
$$ \ left (\ begin 1 0 0 47/4 -13/2 -23/4 \\ 0 1 0 11/2 -3 -5/2 \\ 0 0 1 -39/4 11/2 19/4 \ end \ right) $$
Tehát $ A ^ = \ left (\ begin 47/4 -13/2 02/11 -23/4 \\ -3 -5/2 \\ -39/4 11/2 19/4 \ end \ right) $. Természetesen a megoldás lehet végezni más módon, választott elem a fő átlós. Általában éppen ezt teszi, mert ebben az esetben a végén a döntést, hogy nem kell változtatni a vonal néhány helyen. Adtam az előző döntés csak egy célja van: megmutatni, hogy a vonal választás minden egyes lépésnél nem kritikus. Ha úgy dönt, az átlós elemeket, hogy döntés lenne, mint minden egyes lépés:
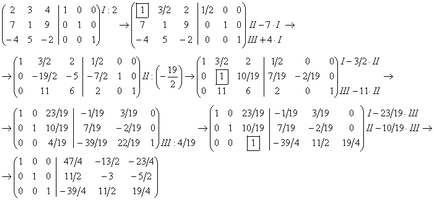
Az utóbbi van egy mátrix: $ A ^ = \ left (\ begin 47/4 -13/2 02/11 -23/4 \\ -3 -5/2 \\ -39/4 11/2 19/4 \ end \ right) $
Inverz módszer Gauss-Jordan kapott csak levelet a válasz továbbra is.
Válasz. $ A ^ = \ left (\ begin 47/4 -13/2 02/11 -23/4 \\ -3 -5/2 \\ -39/4 11/2 19/4 \ end \ right) $.
Keresse meg a mátrix $ A ^ $, ha $ A = \ left (\ begin 1 1 1 0 \\ 2 4 0 1 \\ 0 17 2 \\ -3 -1 4 0 -1 \ end \ right) $.
Az első sor megfelelő nullára ki elemeket az első oszlopban:
A második sor megfelelő nullára ki elemeket a második oszlop:
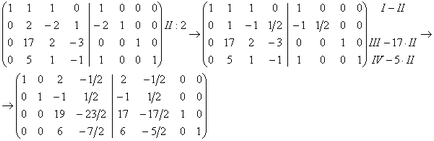
A megfelelő harmadik sorban nullára ki elemeket a harmadik oszlop:

A negyedik sor nulla ki a megfelelő elemek a negyedik oszlop:

Tehát $ A ^ = \ left (\ begin -16/5 -3/5 8/5 2/5 -27/5 \\ 1/5 -1/5 4/5 \\ 19/5 2/5 -7/5 \\ 23/5 24/5 7/5 -12/5 38/5 \ end \ right) $. Ha kihagyja a magyarázatok, a megoldás formájában:

Válasz. $ A ^ = \ left (\ begin -16/5 -3/5 8/5 2/5 -27/5 \\ 1/5 -1/5 4/5 \\ 19/5 2/5 -7/5 \\ 23/5 24/5 7/5 -12/5 38/5 \ end \ right) $.
Ha a megoldása során az átlós elem nullázni meg lehet változtatni a vonal néha. Például, egy mátrixban $ B = \ left (\ kezdődik 1 5 11 10 0 \\ 0 0 9 5 -6 \\ 0 7 1 -1 -3 \\ 0 -11 8 -9 12 \\ 0 0 6 -3 25 \ end \ right) $ megfelelő elemeivel az első oszlop állítani. Szükséges, hogy folytassa a megsemmisítését az elemek a második oszlop, de $ B_ = 0 $. Cserélni a második és a harmadik mátrix sorai a $ B $: $ \ left (\ begin 1 5 11 10 0 \\ 0 7 1 -1 -3 \\ 0 0 9 5 -6 \\ 0 -11 8 -9 12 \\ 0 0 6 -3 25 \ end \ right) $. Most helyett nulla van a 7-es szám és a további folyamatos standard transzformációs módszer Gauss-Jordan elimináció.
Ha érdekel a módszer az inverz mátrix számítás segítségével cofactors, a leírása ez a módszer az első részben.