Elágazás számítási folyamatok - studopediya
Elágazás számítási folyamatok - egy számítási eljárás, amelyben, függően az eredmény ellenőrzése bármely meghatározott feltételek elágazások végrehajtott cselekvési szekvenciák.
1. példa létrehozása számítás áramköri Z = max (X, Y).
A példakénti kiviteli alaknál van két lehetséges válasz: X vagy Y megvalósítási mód kiválasztása kerül sor a vizsgálat eredményét: x> y. Az egyértelműség megoldások úgy vélik, hogy ha X = Y max = X. Általánosságban, a helyét a egyenlőségjel határozza meg a készítmény a probléma.
számítási algoritmus a következő formában:
Részletes számító áramkör képviselt az 1. ábrán. A töredék, mivel a rendszer nem határozza meg egy cselekvési karakterek start, stop, adatbeviteli X, Y.
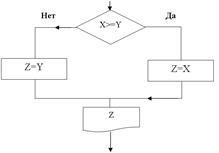
1. ábra. Részletes számító áramkör Z = max (X, Y)
2. példa létrehozása számítás áramköri Z = min (X, Y).
Csakúgy, mint az előző példában, nem lesz két lehetséges válaszokat, és az algoritmus felírható a következőképpen:
Részletes számítási ábrán bemutatott áramkör. 2.
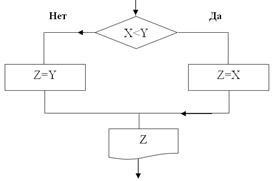
2. ábra. Részletes számító áramkör Z = min (X, Y)
Mindkét algoritmus két ága számítani Z. A jobb oldali ág akkor működik, ha a feltétel teljesül, azaz Igen. A bal oldali ága fut, ha a feltétel sérül, azaz Nem. Ugyanakkor mindkét ág nem fog működni.
3. példa létrehozása számítás áramköri Z = max (A, B, C). Ebben a példában, három lehetséges válasz: vagy A. vagy B. vagy a C. A kiválasztás csak akkor lehet elvégezni az ellenőrzések eredményeit legalább két feltételt, ha egy közbenső használt változó a probléma megoldásában. Következésképpen, a számító áramkör a következőket kell tartalmaznia szimbólumok cselekvési:
Megoldás két karakter. Ellenőrzi feltétele;
Három szimbólum folyamatot. amely hozzá van rendelve egy bizonyos értéket a Z láncot;
Bemutatjuk a közbenső változó R és a következő jelöléseket.
R = max (A, B), majd a
max kiválasztási algoritmus két változó példában tárgyalt 1. példa 1 Ha a címzett bemeneti adatokat, és a válasz, ebben a példában, bevezetett egy további eljárási változó R. A számú bemeneti változók működő bármely alkalmazásban nem korlátozott.
számítási algoritmus a következő formában:
számítási rendszer ábrán látható. 3
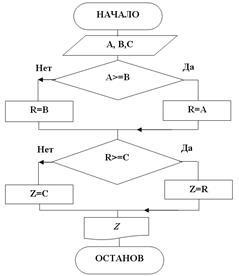
Ábra. 3. A rendszer számítási Z = max (A, B, C). A módszer segítségével a közbenső változó
Vannak más rendszerek számítási legfeljebb 3 változók, például, anélkül, hogy a közbenső változó, de a kör ábrán. 3. a legésszerűbb, t. E. Tartalmazza a legkisebb számú lépésben.
Bár ez a rendszer lehet csökkenteni egy hozzárendelési operátor, ha az R használja közbenső változó kimeneti változó Z és adja R változó, és a következőképpen számoljuk.
Z = max (A, B), Z = max (Z, C)
Változás a rendszer által javasolt magad.