Duhamel integrál - studopediya
Tegyük fel, hogy meg akarja találni a jelenlegi lineáris passzív két terminál hálózat, a tranziens válasz ismert. ha a bemeneti forrás EMF komplex alakú (Fig.44). Kezdeti energiaellátást idején felvételét az EMF nullával egyenlő.

Mi választjuk ki egy tetszőleges rögzített megfigyelési pont t, és ki kell számítani a tranziens áram ebben az időben. Nyilvánvaló, az összeg a jelenlegi ezen a ponton határozza meg a teljes görbe a bemeneti feszültség a t = 0 és a megfigyelés időpontja t. Ezért egy olyan új kijelölése az aktuális időt t. között változik 0 Cserélje sima görbe e (t) lépés, amely indokolja a konstans feszültség e (0) 1 (t) van kapcsolva a t = 0 időpontban. ható az áramkör azon időtartam alatt nulláról ¥. Aztán, miután a T1 időintervallum befolyásolja dE1. Ezután belép a t2 dE2 stb Aztán ..: Hatása alatt az egyes túlfeszültség lép fel az átmeneti folyamat kezdődő a megfelelő időben t. Hatása alatt a komponens e (0) 1 (t) megjelenik az áramkör eleme a jelenlegi i (t) = e (0) h (t). mint a válasz egyetlen funkció tranziens válasz. Miután t1 kitéve DE11 (t - t1) komponens DI1 = DE1 h (t - t1) jelenlegi úgy tűnik, az áramkörben, mint DE1 jár időintervallum t - t1. Az ezt követő időben t2 megint van egy hirtelen változás a feszültség értéke dE2. ami ismét okozhat aktuális összetevő: Di2 = DE2 h (t - t2). Ugyanígy találunk. hogy abban a pillanatban tk okoz egy feszültség ugrás Dek áram Dik = Dek h (t - tk). Alapuló módszerrel összekeverjük a szükséges tranziens áram egyenlő lesz az összege az alkatrészeket találtak a t idő. azaz Annak érdekében, hogy expressziót kapjunk a jelenlegi, változó simán megfelelő bemeneti feszültség, akkor növelni kell az ugrások számának a végtelenig (n ® ¥). intervallumok csökkentése végtelenül dt. Nagysága minden egyes feszültség ugrás de lehet reprezentálni a termék a feszültség változásának mértékét de / dt időtartama ezen intervallum dt. t. e. Az összeg a végállás kapcsolót, és szerves része egy fix időpontban aktuális érték A kapott expressziós hívják Duhamel integrál. A tétel konvolúció funkciók állíthatók elő egy másik kifejezés a Duhamel integrál: 6. példa A bemutatott áramkör az 1. példában kiszámításához a választ a bemeneti impulzus (Fig.45).
Határozat. Ahhoz, hogy megtalálja a tranziens válasz az áramkör kényelmesen használható egy operátor választ. Valóban, a meghatározása szereplő jellemzők, válaszul kép
Másrészt, az áramkör válasz képet a készülék funkciója a bemenő kép egy tranziens válasz
Az 5. példában az átviteli üzemeltető vezetőképességet találtak
,
alkalmazásával, amit találunk a kép a tranziens válasz
Mi jár az eredeti képet bomlási tétel:

A megfelelő görbe h (t) látható Fig.46.

Helyességét ellenőrizni a számítás a tranziens válasz. A t = 0 h (0) nullának kell lennie, mivel a tranziens válasz az aktuális tekercsen átfolyó nulla kezdeti feltételek (törvény alapján kapcsolási áram az induktor nem tudja megváltoztatni hirtelen). Valóban h (0)> 0. Ha t ® ¥ stacionárius rendszer jön létre az áramkörben, egy aktuális I3 = 1 / (R1 + R2 + R3). h (¥) = 0,0125 = i3pr.
Kiszámítjuk az áramkör válasz a bemeneti jel.
Képviseli átmeneti vezetőképesség általában
Az időintervallum 0 TP / 2, az áram az induktivitás
Mivel e (0) = 0, az első kifejezés a kifejezést a szükséges aktuális hiányzik, majd
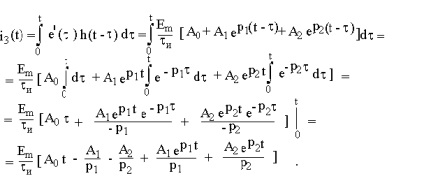
Abban az időintervallum ti / 2 tp.
Továbbá, ha t = TP / 2 bemeneti feszültség hirtelen megváltozott az érték Em / 2.

A t = ti a bemeneti feszültség hirtelen nullára csökken, amely egyenértékű integrálása az EMF állandója ellentétes polaritású, és mennyiséggel egyenlő Em. Következésképpen, a t> tp áramkör választ kell számítani a kifejezést:
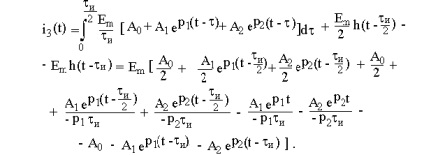
A telek a jelenlegi a induktív ág egy előre meghatározott időben a bemeneti jel látható Fig.47 (arra az esetre, tp = 3 / | P1 |).
