A határozott integrál függvényében a felső határ - studopediya
Tegyük fel, hogy az f (t) van meghatározva, és a folyamatos időközzel tartalmazó pont. Ezután minden x szám ebben az intervallumban lehet a számhoz tartozó,
ezáltal meghatározva az intervallum függvény I (x), amely az úgynevezett határozott integrál változó felső határa. Megjegyezzük, hogy az x = a, ez a funkció nulla. Kiszámítjuk a származékot ezt a funkciót az x. Ehhez először azt a növekmény a függvény x a növekmény az érvelés Dx:
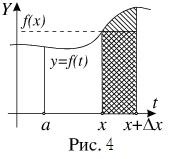
Amint ábrán látható. 4, az érték az utolsó integrál egyenlet a növekmény DI (x) egyenlő a területet a görbe vonalú trapéz jelölt keltetés. A kis dx értékeket (itt, valamint más helyen ez persze, utalva a kis növekmény az érvelés vagy funkció, azt jelenti, abszolút értékeit lépésekben akárcsak a növekmény egyaránt lehet pozitív és negatív), ez a terület nagyjából megegyezik a terület téglalap jelöli az ábrán kettős keltetés. A téglalap területe által meghatározott általános képletű f (x) Dx. Így megkapjuk az összefüggésben
Az utolsó közelítő egyenlőség pontosságának a közelítés nagyobb, minél kisebb érték a DX.
Képlet a differenciálhányados I (X) Ebből következik:
A származék a határozott integrál fölött a felső határ a pont x érték egyenlő az az integrandus ponton x. Ennélfogva, a primitív függvény olyan függvény f (x), ahol az ilyen primitív, amely megkapja a ponton x = nulla értéket. Ez a tény lehetővé teszi, hogy bevezesse a határozott integrál, mint
Legyen f (x) túl primitív az f (x), majd a tételt az általános formája az összes primitívek függvény I (x) = f (x) + C, ahol C - szám. A jobb oldali részén (1) képletű formájában
A képletek (1) és (2) után a változó x, hogy b a képlet a határozott integrál függvény f (t) alatt, az [a; b]:
Ez az úgynevezett formuloyNyutona Leibniz. Itt F (x) - bármely primitív f (x).
Annak érdekében, hogy kiszámítja a határozott integrál függvény f (x) felett, az [a; b] találni olyan primitív F (x) függvény az f (x) és kiszámítja a különbséget primitív értékek a pont b és a. A különbség ezek az értékek általában jelöli a primitív. azaz .
Cseréje egy változó a határozott integrál. A számítástechnikai határozott integrálok segítségével Newton-Leibniz formula előnyösen nincs mereven körülhatárolja lépéseket a probléma megoldására (megtalálása primitív integrandust növekmény megtalálása primitív). Ez a megközelítés, segítségével, többek között, a képlet és cseréje a változó integrálás egy határozott integrált, általában egyszerűsíti a felvétel megoldásokat.
Tétel. Legyen a függvény # 966; (t) folytonos származékot intervallumon [# 945; # 946;], a = # 966; (# 945;), a = # 966; (# 946;), és az f (x) folytonos minden egyes pontja x az x = # 966; (t), ahol t [# 945; # 946;].
Aztán a következő egyenlet alapján:
Ez a képlet az úgynevezett helyettesítő képletű változót egy határozott integrál.
Ahogyan ez volt a helyzet a határozatlan integrál, használja a változás a változó, hogy egyszerűsítse a szerves, így azt a táblázatot (táblázatos). Ebben az esetben, szemben a határozatlan integrál ebben az esetben nincs szükség, hogy menjen vissza az eredeti változót az integráció. Elég, ha megtalálják a határait integráció # 945; és # 946; Az új változó t, mint az egyenletek megoldása ra, t # 966; (t) = a, és # 966; (t) = a. A gyakorlatban kitöltésével változás változó, gyakran kezdődnek a ponton a kifejezést t = # 968; (x) egy új változó a régi. Ebben az esetben, miután megállapította, a határait integráció tekintetében t egyszerűsített: # 945 = # 968; (a) # 946 = # 968; (c).
19. példa Számítsuk
Legyen t = 2 2. Ezután dt = d (2 x 2) = (2 2) „dx = -2xdx és xdx = - dt. Ha x = 0, t = 2-0 = 2 2, és ha X = 1, t = 2-1 = 1 2. ezért:
Integrálás. A módszer integrálás lehetővé teszi számunkra, hogy csökkentsék az eredeti határozatlan integrál egy egyszerűbb formában, vagy szerves része a táblázatban. Ez a módszer a leggyakrabban használt, ha az integrandus tartalmaz logaritmikus, exponenciális, inverz trigonometrikus, trigonometrikus függvények, valamint ezek kombinációi.
A képlet az integráció a következő részekből.
Azaz, az integrandus f (x) dx jelen, mint a termék a funkciók u (x) nad (v (x)) - eltérés a funkció v (x). Következő, azt látjuk, a funkció v (x) (leggyakrabban közvetlen integráció) és d (u (x)) - eltérés a funkció u (x). Behelyettesítve ezeket a kifejezéseket a képlete integrálás, és a forrás redukáljuk határozatlan integrál különbség. Utolsó határozatlan integrál lehet venni bármelyik módszerrel integráció, beleértve az eljárás integrálás.
Példaként találunk egy sor primitívek logaritmus függvény.
Keresse meg a határozatlan integrál
Keressük a határozatlan integrál integrálás. Mivel a függvény u (x) figyelembe ln (x). valamint a d (v (x)) a többi integrandust, azaz DX.
Differenciál funkció u (x). és a funkció v (x) - van.
MEGJEGYZÉS: A C konstans, ha a funkció v (x) nullának tekintjük.
Most már be a képletet integrálás:
.
A legnehezebb dolog ez a módszer - az a helyes, hogy meghatározzák, milyen része az integrandus hogy u (x). és néhány, a d (v (x)).
Tekintsük a standard esetben.
Integrálok a formában, vagy. ahol - polinom foka n. egy - koefficiens függvényében u (x) polinomot választott.