Az inga Maxwell
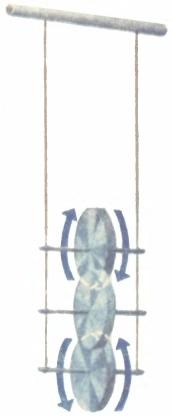
Nézd meg a képet a inga. Ez a lemez van szerelve a tengely, amely a két szál kapcsolódik. A felső végükön vannak rögzítve a kapufáról. Húzzuk meg a menet egy tengely körül - drive emelkedik. Most engedje az inga -, és elkezd csinálni periodikus mozgásra: első lemez csökken, a szál letekerjük, a lemez gyorsabban forog; elérve a legalacsonyabb pont, és továbbra is forgatni a tehetetlenség, a hajtás megváltoztatja a mozgás irányát és emelkedik. Tehát ingadozik ütközésig.
Néhány ötlet a inga lemezen kell lennie a nehéz ($ m> $ 100 g), egy nagy ($ d> $ 5 cm) tengelyen - egy vékony és könnyű, a szál - tartós és elég hosszú ($ 0,5 $ m). Sokkal jobb, hogy van egy sor olyan hajtások, én a tengelyen.
Ez könnyű kitalálni, hogy az időszak oszcilláció az inga, azaz a. E. A teljes ideje süllyedési és emelkedési, nem függ a tömeg a lemez, és függ a sugár, és ez a függőség szinte egyenesen arányos. Ez azt jelzi, hogy szükség van az ilyen dolog, mint a tehetetlenségi nyomaték J $ $ (lemez $ J = mr ^ 2/2 $), hogy leírja a mozgását egy inga.
A pontos képlet a Maxwell inga periódus állítható elő viszonylag egyszerű számítások (lásd. Például „Quantum” Journal 1981 №11).
ahol $ l $ - hossza az izzószál, $ R $ - a korong tengelye sugara, $ J $ - a tehetetlenségi nyomaték.
Ez a képlet lehet alkalmazni, hogy a lemez, és egy gömb, illetve megváltoztatásával az inga szerkezetét.