Az elmélet arányok építészet, építész Felsőoktatási
Informregistr azonosító szám: 0420600020 \ 00
Jelenleg különböző elméletek arányok, ami együtt járt az architektúra minden szakaszában a történelem. A lényege minden arányban fogalmak - létrehozunk egy törvényes rend, amely miatt a készítmény egység és harmónia.
Bevezetés bármilyen mintát (numerikus, geometriai) fogalmához kapcsolódó különféle szimmetriák (statikus, dinamikus, stb.)
A cikk ismerteti az elméleti építészeti tervezés, épül alapján a dupla szögletes, így menekülni eltérő arányban.
Művészi hatás klasszikus szimmetrikus kompozíciók oka, hogy a valódi építőiparban a modult. Az emberek idegesen reagálnak az épület úgy tűnik kiegyensúlyozatlan vagy fejnehéz. És nem azért, mert akkor esik számunkra, hanem azért, mert az emberek mentálisan hiszen vetített maga az épület saját testét korrelál body building. A izmok fájnak, amikor láttam a nehéz párkány, izmaink feszült fel a szimpátia, amikor egyensúlyhiányt észlel az építészeti kompozíció. Ez az úgynevezett tudattalan mimetikus ösztön tesz minket asszimilálni magukat látszólagos súlya, nyomás, ellenállás, bemutatott formában, amelyek látható, azaz Más szóval, van a „vzhivaemosti” a szerkezete az épület.
A koncepció a relatív egyenlőség jár megértését geometriai minták, ha meg lehet osztani maradék nélkül egyenlő részekre vonatkozóan a geometriai jellemző, például az építési mód. Felvételi geometriai minták végezhetjük számok formájában, vagy képletek.
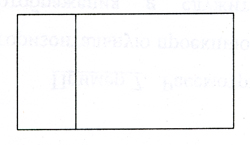
Különböző arányban az elmélet az építészet kíséretében minden szakaszában a történelem. A lényege az összes fogalmak arányban - annak érdekében, hogy a lefektetett törvények, amelyek hatására a készítmény egység és harmónia. A fogalom olyan törvényeket, numerikus, geometriai, szerepel a fogalom a szimmetria. Koncepciója alapján a geometriai minták, tudjuk építeni a „dinamikus” szimmetria. Egy alapján statikus szimmetria kiválasztotta a megfelelő geometriai forma. Ismeretes, hogy az arány a saját oldalán képviseli racionális számok és irracionális kapcsolatát azok elemeinek vannak kialakítva az átlós négyzetes (V - 2) és a mellékhatások (egységét). Így téglalapot az épített terület V - 2. Ezután, az átlós és az oldalán az eredeti téglalap van kialakítva, amelyek a négyzet V - 3 stb (1. ábra).
1. ábra. - Dinamikus Rectangles
Ez a konstrukció lehet végtelenségig folytatható.
A területet a téglalap V - 5 szolgál alapján a legjobb megvalósítási módja a dinamikus szimmetria.
Az elmélet az építészeti tervezés mindenkor nagyon fontos. Például, amikor meghatározzuk a boltíves teret magasságot használnak csak aritmetikai, geometriai és átlagos oldalaránya. Emlékezzünk, meghatározva ezen eszközökkel. A sorszámok a1. a2. a3. a4 ... ez az úgynevezett egy számtani sorozat. Ha a különbség bármilyen számú és a következő állandó: a2 - a1 = a3 - a2 = a4 - a3 = .... Például, az 1, 3, 5, 7, 9 ... alkotnak számtani sorozat. Mindenesetre számtani sorozat a3 = A1 + 2a2. a2 + a4 = 2a3, ... stb Tehát, más szóval, minden szám felével egyenlő összegű szomszédos számokat. Minden egyes tagja a számtani sorozat az úgynevezett átlagos szomszédos számok. Így kapunk egy szabály kiszámításához számtani átlaga kétjegyű szám a és b. amely egyenlő: (a + b) / 2.
Ha egy számsorozat a1. a2. a3. ... a4 megvan az a tulajdonsága, hogy minden tagja vonatkozásában az előző sorrend folyamatosan a2 / a1 = a3 / a4 = a2 / a3 .... Egy ilyen szekvenciát nevezzük mértani. Ebben az esetben, a1 = a3 × (a2) 2. a2 = a4 × (a3) 2. ... így minden egyes tagja egy mértani négyzetgyöke a termék két szomszédos számok és a geometriai átlag két szám a és b képlettel számítottuk ki V - ab .
A sorszámok a1. a2. a3. ... a4 az úgynevezett harmonikus progresszió. ha a sorszámokat, adatokat az inverz 1 / A1. 1 / a2, 1 / a3. ... képez egy számtani sorozat. Bármely tagja egy ilyen sorozat az úgynevezett harmonikus átlaga két szomszédos tag, azonban annak érdekében, hogy megtalálják a harmonikus átlagát két szám a és b. először megtalálni a számtani átlaga inverzeinek számokat, majd a kölcsönös ez az átlag. Így a harmonikus közép értéke: 2ab / (a + b).
Püthagorasz volt az első, aki észreveszi, hogy a pályán által kibocsátott feszes húr, általában hosszával arányos a húr. Ha húzza a húr feszes, majd nyomja meg a középső ujját, és ismét húzzuk, akkor a hang által kibocsátott húr másodszor lesz egy oktávval magasabb, mint az első. Ha megnyomja a húr, és ingadozik csak egyharmada eredeti hosszának, a frekvencia által kibocsátott hangon háromszor alapfrekvencia. Ettől kezdve világos, hogy milyen fontos a harmonikus szekvencia által alkotott reciprok tagjai egy számtani sorozat. Természetesen a legegyszerűbb szekvenciák harmonikus formában van 1, 1/2, 1/3, 1/4, ...
Egy másik elmélet az építészeti tervezés alapja egy dupla szögletes.
Két négyzetek, halmozott alkot egy dupla szögletes. Hozzáadjuk a két dupla szögletes, azt látjuk, a tér, ismétlődő alakját eredeti téren. Ez egy egyszerű additív tulajdonsága négyzet széles körben használják az építészet, a reneszánsz.
„Aranymetszés” volt ismert építészek a reneszánsz, de nem azt hatékonyan használni, mint egy eszköz beszerzése arányokat. „Aranymetszés” Luca Pacioli úgynevezett isteni arányban. Az „aranymetszés” Németországból származik az első felében a XIX. és adja meg
m = (1 + V - 5) / 2