aszimptotájának a görbe

Referenciák: [3], Ch. V, § 10

Közvetlen úgynevezett aszimptotájának a görbe y = f (x), ha a távolság M pont az egyenes vonal görbe nullához, mint az M pont a görbe mentén a végtelenbe a származási (ábra. 1.7).

Különbséget tenni a függőleges és ferde aszimptota. A függőleges asymptote van egy egyenlet az x = x0, és egy vonal párhuzamos a tengellyel Oy. Ferde aszimptota egyenlet formájában y = kx + b. Abban a különleges esetben a k = 0 az úgynevezett vízszintes aszimptóta, mint a y = b egy vonal párhuzamos Ox.

Legyen egy görbe y = f (x). Ahhoz, hogy megtalálja a függőleges aszimptotáját a görbe pontok végtelen a törés (töréspontok a második fajta).

majd az egyenes vonal az x = x0 ─ függőleges aszimptotájának a görbe y = f (x) (ábra. 1.8).

Ferde és vízszintes aszimptota.

Tegyük fel, hogy egy görbe y = f (x). Ahhoz, hogy megtalálja a ferde aszimptotákkal amelynek egyenlete y = kx + b, együtthatók k és b. kiszámítása határok:

,. Ezek a határértékek kiszámítása külön esetekben

és

. Ha legalább egy a korlátai vychisleniyak és b értéke ∞ vagy nem létezik, akkor a görbe meredeksége és a vízszintes aszimptota nem.

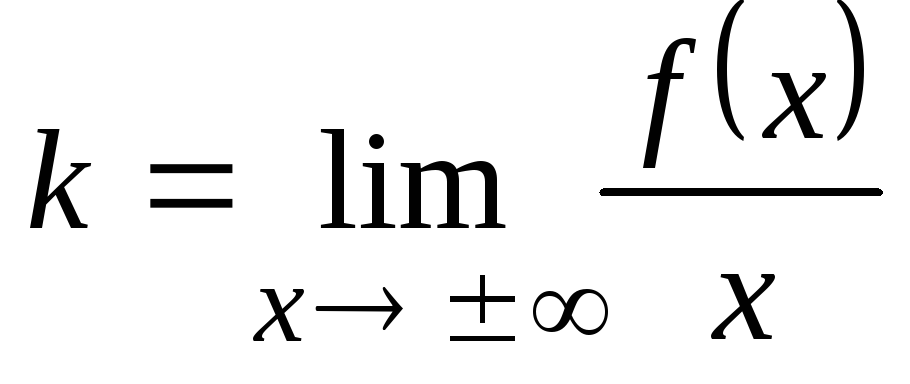
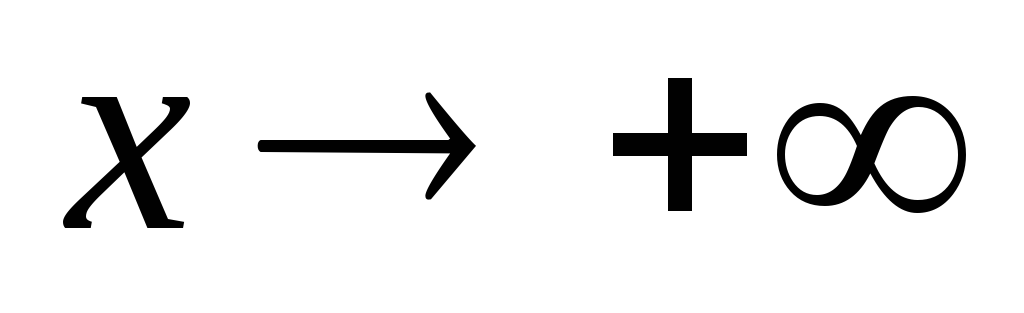
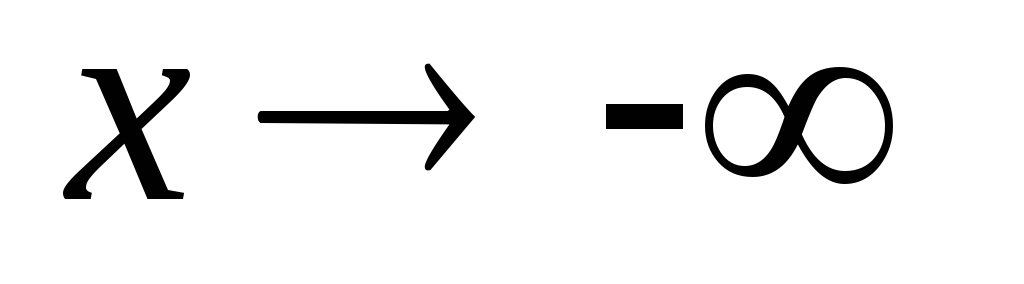
Abban a speciális esetben, ha k = 0, és b ─ véges számú, a görbe vízszintes asymptote amelynek egyenlete y = b.

Példa. Keresse meg a aszimptotája a görbe

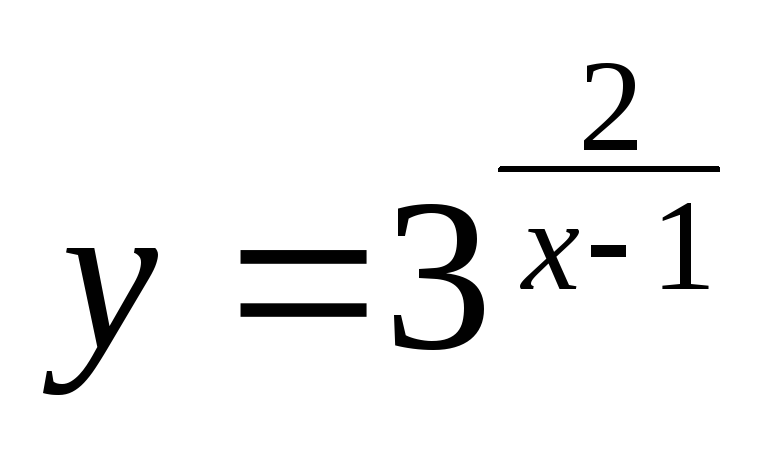
Határozat. függvény

Úgy felvette az egész készlet érvényes chiselR. kivéve a x = 1. Mi határozza meg a rés jellegű, amely kiszámítja a határok a függvény az x → 1, a bal oldalon (x <1) и справа (x> 1):

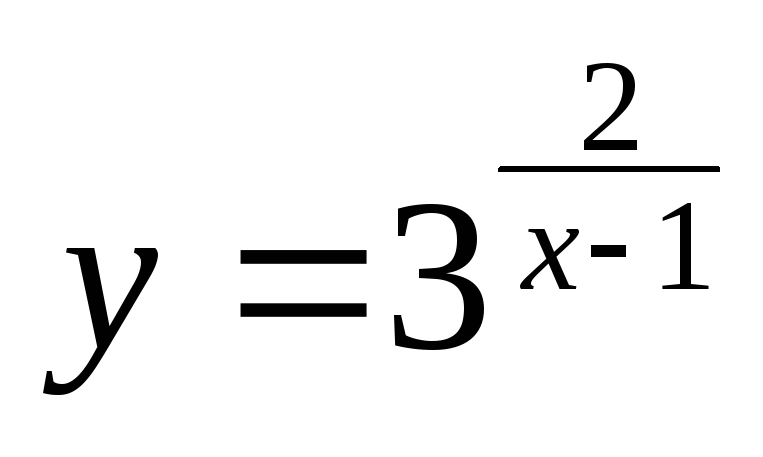
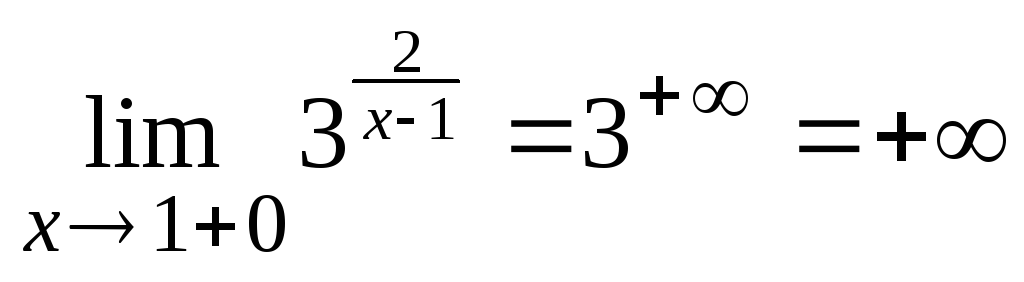
Mivel az egyik korlátok végtelen, X = 1, egy pont a folytonossági hiány a második fajta, és így, a görbe egy függőleges asymptote x = 1.

Határozza meg, hogy a görbe egy ferde vagy vízszintes asymptote. Ahhoz, hogy ezt elérjük, kiszámítja a megfelelő határok között:

, Egyenlet asimptotyy = kx + b az y = 1 (vízszintes asymptote).

hematichesky függvény grafikonját ábrán látható. 1.9.

1.14. Vezetési teljes körű vizsgálatot a funkció és az építőiparban a grafikon

Referenciák: [3], Ch. V, § 11

1. Keresse meg a domain a funkciót.

2. Állítsa be a paritás páratlan függvény, periodicitás. Találunk a jellegzetes pontok, mint például metszéspont a koordináta-tengely.

3. Keresse meg azt a pontot a diszkontinuitás a funkciót, akkor határozza meg a karakter. Ha egy második típusú break pontot (pontokat diszkontinuitás a végtelen) készlet rendelkezésre állás diagram függőleges aszimptotákkal.

4. Keresse meg a függvény deriváltját, a kritikus pontok, időközönként monotonitás, szélsőérték a pont és a függvény értéke ezeken a pontokon.

5. meg a második függvény deriváltját, a időközönként domborulat van és konkáv görbe, és az inflexiós pont a grafikon a funkciót.

6. Állítsa be a jelenlétét a vizsgált görbe ferde és vízszintes aszimptotákkal.

7. A kapott adatokból a grafikon épít.

Megjegyzés. Ha egy függvény páros vagy páratlan, a vizsgálatot úgy végezzük, nem a teljes valós tengelye és a [0, + ∞). Ezután továbbra is gráf szimmetrikusan az ordináta időközönként (-∞, 0), ha egy még funkciót, és a relatív, hogy a központ a koordináta-rendszer, ha páratlan funkciót.

Ha a funkció periodikus, a grafikon épített egy időszakra, majd továbbra is periodikusan teljes tengelyre.

Példa. Hogy végezzenek teljes tanulmányt a funkció

és konstrukció a grafikon.

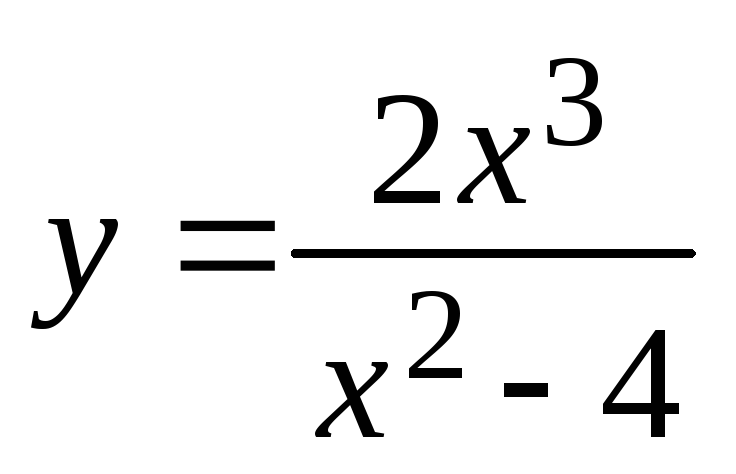
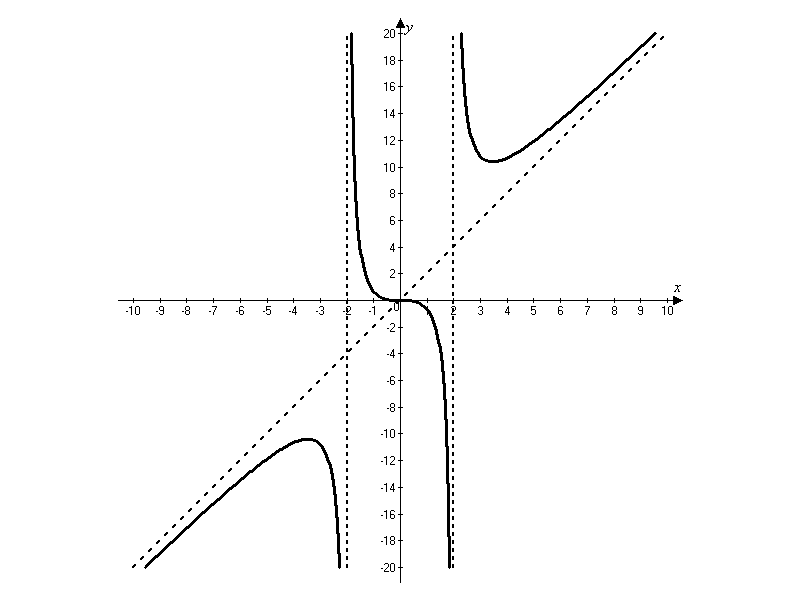
1. A függvény és folyamatos az egész valós tengelye, kivéve azokon a pontokon x = ± 2.

2. A funkció páratlan, mint a feltétel érte. Ezért elegendő, hogy készítsen tanulmányt a [0, + ∞).

3. A [0, + ∞) egy töréspontot x = 2 természetének vizsgálatára break pontot, amely kiszámítja a következő határértékeket:

Mivel az egyoldalú határértékek végtelenek, a vonal x = 2 egy függőleges aszimptota.

4. Keresse meg az első derivált:

Találunk a kritikus pont a [0, + ∞):

. Annál a pontnál

származék nem létezik, de ezen a ponton nem kritikus, mivel a funkció nem az ott meghatározott.

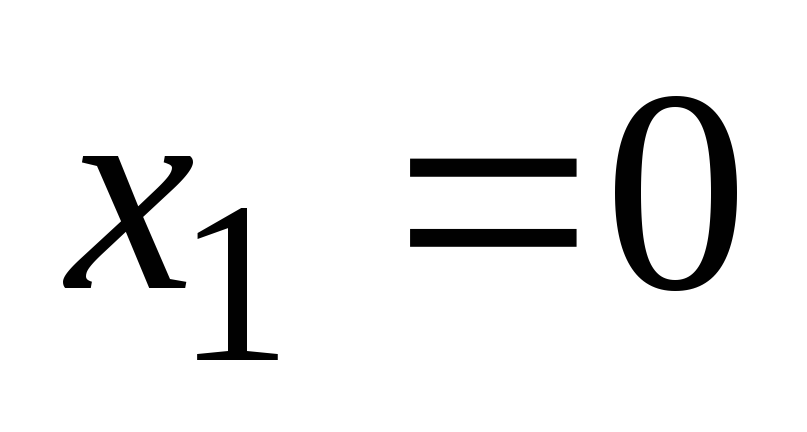
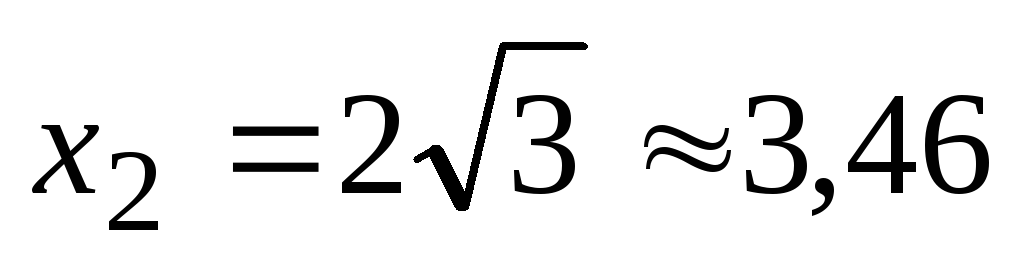
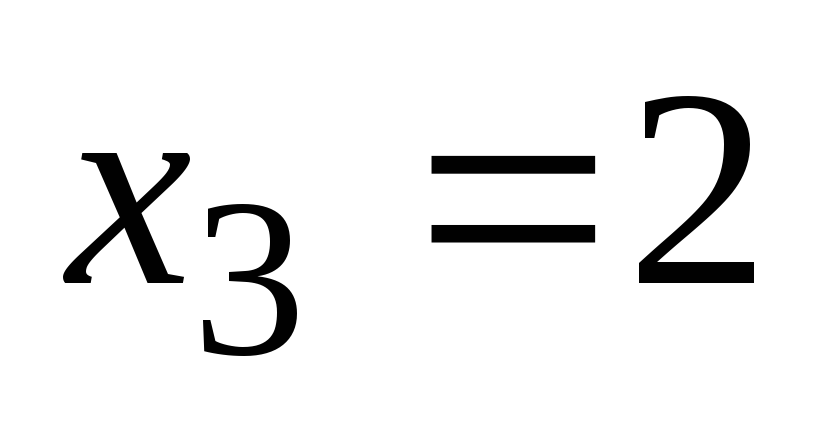
5. Keresse meg a második derivált:

A második derivált a [0, + ∞) nullává válik azon a ponton, x1 = 0, és van pontjában x3 = 2, amely nem szerepel a funkció tartomány.

A kapott adatokat az épület egy táblázatot:

Az első sorban a táblázat meghatározott időközönként, amelyek esetében a kritikus pont, és a pont, ahol a második derivált nullával egyenlő vagy nem létezik, felosztják a [0, + ∞). A második sorban a jele az első derivált ezen intervallumok, a harmadik - a jele a második derivált. A negyedik sor ábrázolja önkényesen kell növelni vagy csökkenteni a funkció az intervallum (a jel szerint, az első derivált), és a konvexitás vagy konkáv görbe (a jele a második derivált).

6. keresünk egy ferde asymptote:

A görbe a [0, + ∞) van egy ferde asymptote

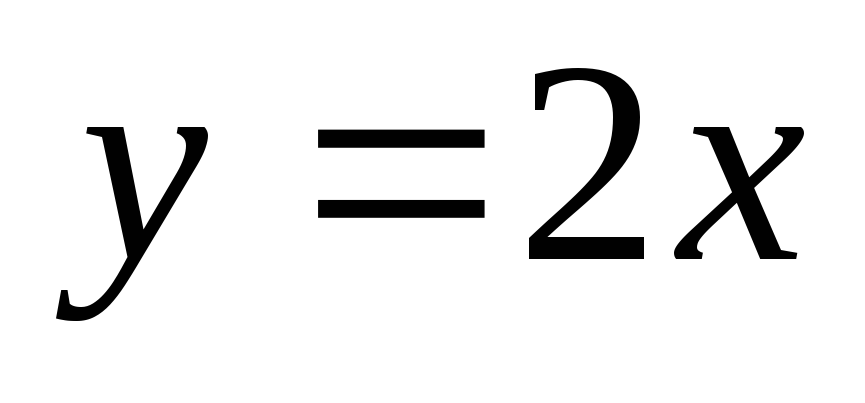
Épület függőleges X = 2 és y = 2x ferde aszimptotákkal, majd a táblázat adatai össze egy grafikon a funkciót a [0, + ∞), amely azután tovább az intervallum (-∞, 0) szimmetrikus a központja a koordináta-rendszer.

Kapcsolódó cikkek

előző ◈ a következő