Aszimptotájának a görbe - studopediya
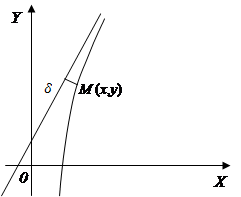
Függőleges asymptote ott, viselkedését mutatják be a funkciót a szomszédságában szinguláris pont, amikor, és ferdén, így egy ötlet a viselkedését a funkciót.
Ha a szinguláris pont, az egyenlet a függőleges asymptote.
Tétel. A görbének van egy ferde aszimptótát meg, amelynek egyenlete, ha véges érték és elfogadom.
Bizonyítás. A meghatározás követi aszimptotákkal ahol elenyésző a, azaz a. Továbbra is paraméterek meghatározásához az egyenlet a asymptote. Ehhez értékeljük. Így, ha a két szélső létezik, és végesek, és a vonal paraméterei határozzák meg, a pont ennek összhangban pontok végtelenül konvergáló görbe.
Példa. . Nyilvánvaló, hogy - a függőleges asymptote egyenlet.
.
Ferde asymptote egy egyenletet.
Tanulmány a funkció, az építési ütemtervet,
I. Tanulmány a funkciót is. telepíteni kell
1) A domain a funkcióját, egyes pontokat, függőleges aszimptotákkal.
2) A metszéspontja a görbe koordinátatengelyeken
3) A funkció páros, páratlan, vagy általános formája
4) A funkció periodikusan ismétlődő vagy nem periodikus
II. Egy tanulmány differenciálhányados. Meg kell határozni, hogy
1) a maximális pontot, és minimális funkciókat
2) időközök növekedését és csökkenését a függvény
III. A tanulmány a második derivált
1) Az inflexiós pontok
2) Az intervallumok konvexitás és konkáv
IV. Tanulmány a viselkedését a funkciót. Ferde asymptote.
Példaként tekintsük a funkció
1. Mező létezésének függvénye - az egész valós tengelye, azaz a. Ezért ez a görbe nem az egyes pontokat, és nem függőleges aszimptotákkal.
2. A görbe metszi a koordinátatengelyek a származási. Következésképpen, az első jellemző pontot a grafikon.
3. A görbe furcsa: így ez szimmetrikus az eredetét.
4. A nem-periodikus függvény.
II. 1. Mi határozza meg az első származék, ami átszámítva ez nulla, ami azt jelenti, két specifikusabb (kritikus) pont koordinátáit ezek pont a síkon. Vegyük az első ilyen pont, balra származéka, az a jobb, ezért ezt a minimális pontot. Ahhoz, hogy a bal oldalon a származék jobb negatív, akkor ez az a pont a maximum funkciót.
2. A jel az első derivált határozza meg a kifejezés, így ez pozitív időintervallumra, más területeken az negatív. Így a funkció csökkenti az intervallumot, az intervallum növekszik, majd csökken vissza.
III. 1. Határozza meg a második függvény deriváltját:
.
Azonosítjuk a származék nulla, és megkapjuk a három jellemző pontjait a funkció, amelyek közül az egyik már ismert. És a másik kettő. ezek a koordináták egy koordinátarendszerben. A jel a második derivált határozza meg a számláló. Ahhoz, hogy a bal oldalán negatív, a jobb oldalon. Ezért ez egy inflexiós pontja. Elhagyták a jobbra. Egy másik inflexiós pont. Balra a ponton eljutunk a jobb oldalon, a harmadik inflexiós pontban.
2. Mivel a többi pontok, ahol a második deriváltja elõjelet a funkció nincs jelen, azt lehet mondani, hogy a tartomány egy konvex görbe, konkáv görbe az intervallum, az intervallum konvex görbe újra, és végül, az intervallumban - homorú.
IY. Meghatározása a lejtőn a aszimptotájának a görbét, egyenletet asymptote, ahol
,
,
Mivel egyenlet aszimptóta a aszimptota funkció a tengelyt.
Ennek eredményeként, a grafikon formájában
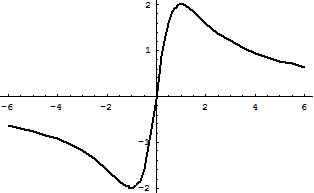
Az ábrán jól megfigyelhető minimális és maximális pontot és funkciók három inflexiós pont. Is látható, hogy a görbe „nyomott”, hogy a tengely hajlamos mind a plusz és mínusz végtelen és következésképpen egységes asymptote.
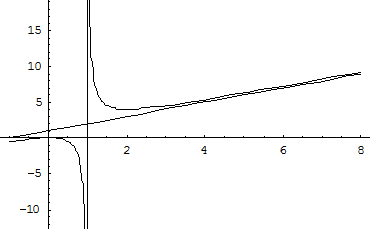
Vegyünk egy példát a különböző tervezési eredményt. Let. A régió létezik ez a funkció - a teljes valós tengelye mellett a lényeg. Aperiodikus függvény (nincs trigonometrikus függvények), általános formája (még nem igaz).
Először határozza meg az összes jellemző pontjait a grafikont, azaz a metszéspontja koordinátatengelyeken, egyes pontokat, maximális és minimális pontot, inflexiós pont. Erre a célra kiszámítjuk az első és a második deriváltak
,
.
Feltárása a funkció és származékai, megállapítjuk, hogy van egy szinguláris pont, és három jellemző pontok ,.