Algebra osztály 8, osztály, hogyan kell építeni egy grafikonon az f (x) m
Az előadás és a leckét a témáról: „Hogyan építsünk egy grafikonon az f (x) + m”
Srácok, ma megtanuljuk a másik módszert alkalmaztuk, grafikonok funkciók!
Mi eljárni, mint az előző leckében konstrukció azonos koordináta rendszerben három parabola: $ y = x ^ 2 $, $ y = x ^ 2 + 3 $, $ y = x ^ 2-3 $.
A grafikon az első függvény jól ismert, a többi össze egy táblázatot az értékek. $ Y = x ^ 2 + 3 $.
$ Y = x ^ 2-3 $.
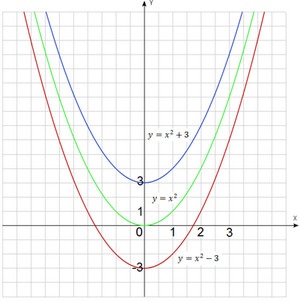
$ Y = x ^ 2 $ - zöld, $ y = x ^ 2 + 3 $ - Blue, $ y = x ^ 2-3 $ - piros.
Talán észrevetted, hogy a grafika gyakorlatilag azonos. Mindegyikük lehet beszerezni a hagyományos parabola tolódott felfelé vagy lefelé. Kaptunk egy ábrázolási eszköz szinte megegyezik az egyik, hogy volt az utolsó óra. Ez megkönnyíti az építkezés sok más grafikonok a funkciók.
Írunk az általános szabály:
A konstrukció a grafikon a $ y = f (x) + m $, ahol $ m $ - mondta pozitív számok szüksége grafikonja $ y = f (x) $ eltoljuk $ m $ egységek felfelé az ordinátán.
A konstrukció a grafikon a $ y = f (x) -m $, ahol $ m $ - mondta pozitív számok szüksége grafikonja $ y = f (x) $ eltoljuk $ m $ le egységek az ordinátán.
Más szóval, ha egy számot adunk, a grafikon felfelé eltolt, ha levonjuk a grafikon lefelé lép.
1. példa.
Szerkesszünk egy olyan grafikont a funkció: $ y = -4x ^ 2 + 2 $.
Határozat.
Ütemterve a funkció nyert grafikon $ y = 4x ^ 2 $. Ez egy parabola felfelé eltolt két egység.
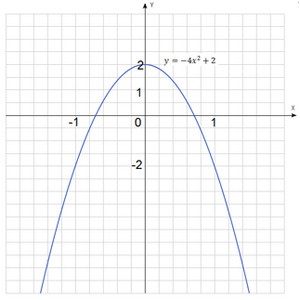
Srácok, figyeljen a skála a grafikon. Mi lehet választani magadnak, hogy menetrend gyönyörű volt!
2. példa.
Szerkesszünk egy grafikont a funkció: $ y = \ frac + $ 3.
Határozat.
Ütemterve a funkció nyert grafikon $ y = \ frac $. Ez túlzás által kiszorított három egység fel.
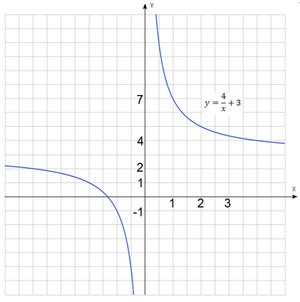
Segítségével a szerszám, akkor nem csak építeni grafika, hanem oldja meg sok más kapcsolódó problémák menetrendek.
3. példa.
Keresse meg a legkisebb és a legnagyobb értéke $ y = 3x ^ 2 + 1 $ a szegmens $ [- 1, 2] $.
Határozat.
A legkézenfekvőbb módja, hogy megoldja ezt a példát, hogy létrejöjjön egy megfelelő ütemtervet.
Ütemterve a funkció nyert grafikon $ y = 3x ^ 2 $. Ez a parabola felfelé tolódott egy egységgel. Piros színnel kiemelve intervallum, amelyen szeretné megtalálni a minimum és maximum értékeket. A legalacsonyabb pont a kiválasztott terület egybeesik a legalacsonyabb érték, a legmagasabb pont - a legmagasabb érték.
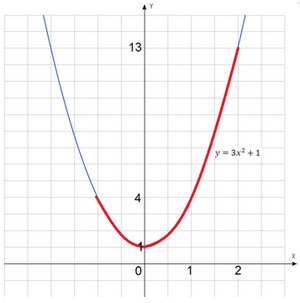
A legalacsonyabb pont az Y-tengely egyenlő eggyel, és a legmagasabb pont elérésekor a ordináta 13. Ezek a legalacsonyabb és a legmagasabb értékek. $ Y_ = 1 $, $ y_ = $ 13.
4. példa.
Megoldani az egyenletet: $ x ^ 2 + 1 = \ frac-2 $.
Határozat.
Mi megoldjuk az egyenletet grafikusan. Készítünk két grafikont funkciót, és megtalálja a metszéspont.
$ Y = x ^ 2 + 1 $ - parabola felfelé tolódott egy egységgel.
$ Y = \ frac-2 $ - hiperbola, által kiszorított két egység lefelé.
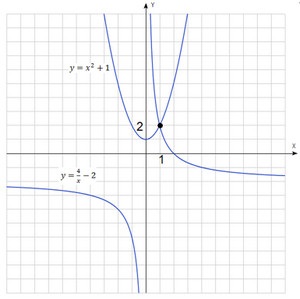
A metszéspont egy koordináta $ (1; 2) $. Meg kell koordinátáit $ x $.
Válasz: $ x = 1 $.
5. példa.
Építsd és olvassa el a függvény grafikonját: $ y = \ kezdődik (x-3) ^ 2, 0hozzászólás
Kapcsolódó cikkek