Alapvető módszerek integrációját
1. Közvetlen integráció
Közvetlen integrációt megvalósítani egy ilyen módszer az integráció, ahol az integrált átalakulás azonos integrandust és használata a határozatlan integrál tulajdonságai az, hogy egy vagy több táblázatos integrálok.
1. példa Find
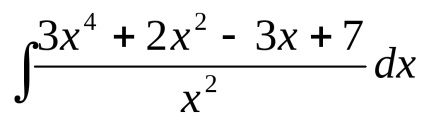
osztás számlálója a nevező, megkapjuk:
=
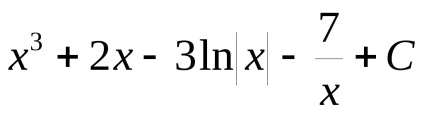
Jegyezzük meg, hogy nem szükséges, ha minden távon beállítani egy tetszőleges konstans úgy, hogy az összegük is tetszőleges konstans, hogy írunk a végén.
2. példa keresése
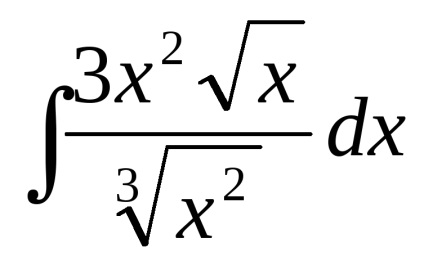
átalakítsa a integrandust a következőképpen:
.
Alkalmazása a táblázatban integrál 1, megkapjuk:
.
.
.
=
=.
Bizonyos esetekben, megtalálni a szerves egyszerűsíti a mesterséges módszerekkel.
6. példa Find
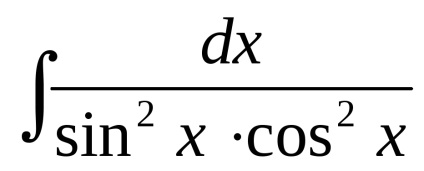
megszorozzuk az integrandus találni
= .
.
.
2. Az integráció helyett változó
Számolja adott szerves közvetlen integráció nem mindig lehetséges, és néha ez általában nagy nehézségbe ütközik. Ezekben az esetekben más technikákat. Az egyik leghatásosabb módszer a változó módosítása. Ennek lényege abban rejlik, hogy bevezetésével egy új változót az integráció lehet csökkenteni adott szerves része az új, ami viszonylag könnyen közvetlenül. Kétféle változatban ez a módszer.
a) módszer összeadási műveletet jel alatt az eltérés
A meghatározása differenciál.
Ebbe az egyenletet balról jobbra az úgynevezett „összeadásával faktor
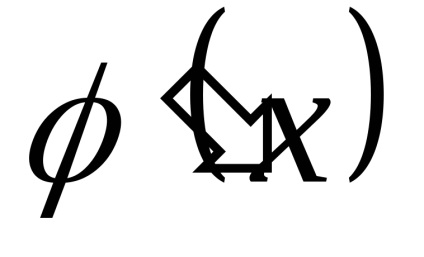
Tétel az invariancia az integrál képletek
Minden integrációs képletű megtartja formáját, amikor a helyére a független változó bármely differenciálható függvénye, azaz, ha
ahol
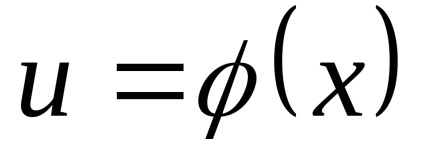
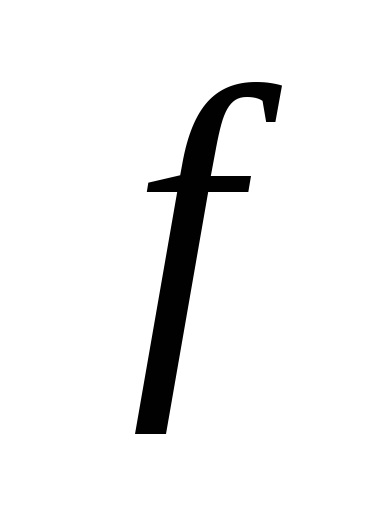
Minek kellene
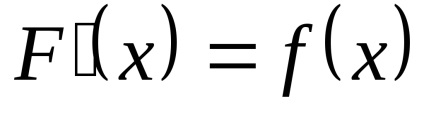
.
Tegyük fel, szeretnénk számítani az integrál
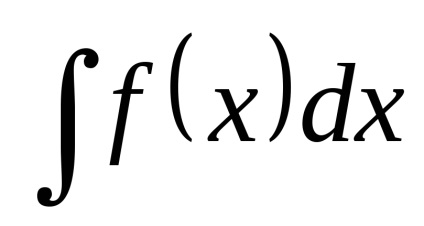
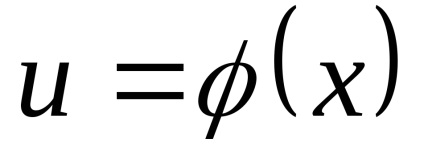
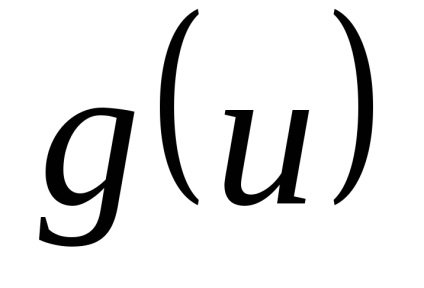
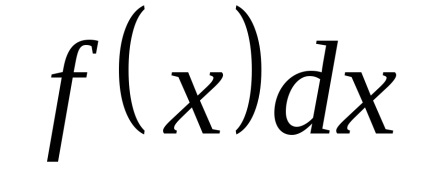
.