A távolság egy pont, hogy egy egyenes vonal a térben - elméletben, példák, oldatok
Tegyük fel, hogy a háromdimenziós térben rögzített derékszögű koordináta-rendszert Oxyz. adott egy pont, egy egyenes vonalat, és azt szeretné, hogy megtalálják a távolság pont a vonal.
Megmutatjuk a két módszer, amely lehetővé teszi, hogy kiszámítja a távolságot egy pont a vonal az űrben. Az első esetben a távolság M1 megállapítás arra utal, hogy egyenesen csökken megtalálni a távolság a pont M1 pont H1. ahol H1 - a bázis a merőleges a tochkiM1 közvetlen a. A második esetben a távolság egy pont síkra fog találni, mint a magassága a paralelogramma.
Az első módszer a megállapítás a távolság a pont a vonal az űrben.
Mivel definíció szerint a távolság a lényeg, hogy sorban M1 a - hosszúság perpendikulyaraM1H1. Ezután meghatározzuk a koordinátákat a pont H1. tudjuk számítani a szükséges távolságot a két pont közötti távolság, és a képlet.
Így a probléma csökken megtalálása egy bázis koordináta merőleges épített attól a ponttól, M1 az egyenes vonal a. Legyen egyszerű: a lényeg H1 - a metszéspont a vonal egy átmenő sík M1 pont merőleges vonal.
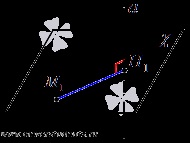
Következésképpen az algoritmus határozza meg a távolság tochkido pryamoyav helyet. a következő:
Alkotunk az egyenlet, mint a gép egyenlete áthaladó sík adott pont merőleges az adott vonalat;
Mi határozza meg a pont koordinátáit H1 - a metszéspont a vonal és sík (lásd a cikk megtalálása koordinátáit a metszéspont a sor, és amely sík);
Mi kiszámítja a szükséges távolság a pont M1 egy egyenes vonal, amelyet a képlet.
A második módszer megtalálására a távolságot egy pontot egy egyenes vonal a térben.
Mivel a probléma adott egy egyenes vonal. meg tudjuk határozni annak irányát vektor és a egy pont koordinátáit M3. feküdt az egyenest a. Ezután a pontok koordinátáinak, és ki tudjuk számítani a koordinátákat a vektor: (ha szükséges, lásd a cikk, a koordinátáit a pontok koordinátái annak kezdete és vége).
Elhalasztja vektorok és M3 pontot és megépíteni őket paralelogramma. Ez paralelogramma ráfordítási magasság M1H1.
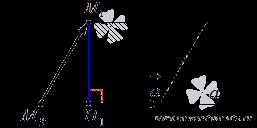
Nyilvánvaló, hogy a magassága a paralelogramma van kialakítva M1H1 kívánt távolságot tochkiM1 hogy a vonal egy. Found.
Az egyik oldalon a paralelogramma terület (jelöljük S) megtalálható cherezvektornoe termék a vektorok és a képlet. Másrészt a terület egy paralelogramma egyenlő a termék a hossza az oldalán, hogy a magasság, azaz amelyben - a vektor hossza megegyezik a hossza a figyelembe vett oldalán a paralelogramma. Ezért a távolság egy előre meghatározott ponton M1 adott vonalon megtalálható a egyenlőségét mindkettő.
Tehát, hogy megtalálják a távolság tochkido pryamoyav helyigény
határozza meg az irányt vektor a vonal a (), és kiszámítja a hossza;
így a egy pont koordinátáit M3. feküdt az egyenest a. koordinátáinak kiszámításához vektor, megtalálja a vektor termék, és hogyan lehet, és hossza;
kiszámítja a szükséges távolság egy pont egy sorban a térben a következő képlet szerint.
Problémák megoldása megtalálni a távolság egy adott ponton az adott vonalon az űrben.
Vegyük példának a döntést.
Keresse meg a távolság pont vonal.
Írunk az egyenlet a sík ponton áthaladó merőleges az adott sorban M1:
Megtaláljuk a pont koordinátáit H1 - a metszéspont a sík és egy előre meghatározott egyenes vonal. Ehhez hajtsa végre az átmenetet a kanonikus egyenletek egy egyenes vonal az egyenletek két egymást metsző síkok
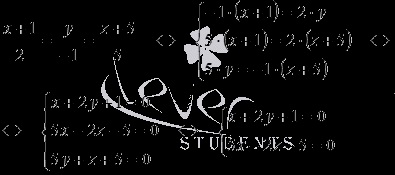
majd megoldjuk a lineáris egyenletrendszer Cramer:

Továbbra is számoljuk ki a szükséges távolság a pont az egyenes, mint a pontok közötti távolság u :.
A számok a nevezőben a frakciók a kanonikus egyenes egyenlete a megfelelő koordinátái az irányvektor az egyenes vonal, azaz - az irányvektor a sor. Számolja hossza :.
Nyilvánvaló, hogy a vonal áthalad egy pontot, majd a vektor kezdeti pont és a végpont ott. Találunk a kereszt termék vektorok:

Most már az összes adat, hogy használja a képlet a távolság egy adott pont egy adott síkon :.
.
A kölcsönös elrendezése vonalak térbeli