A rendszer lineáris egyenlőtlenségek és konvex ponthalmaz
Egyenlőtlenség - két számot vagy matematikai kifejezések, csatlakozik az egyik karakter:> (nagyobb, mint abban az esetben, szigorú egyenlőtlenségek) <(меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Egyenlőtlenség lineáris ugyanolyan körülmények között, mint az egyenlet: tartalmaz egyedüli változó az első fokú, és nem tartalmaz termékeket változók.
Megoldás lineáris egyenlőtlenségek és rendszerek lineáris egyenlőtlenségek elválaszthatatlanul kapcsolódik a geometriai jelentés: lineáris egyenlőtlenség megoldás néhány félig sík, amely sík osztja az egész sort, amelynek egyenlete meghatározott lineáris egyenlőtlenségek. Ez félsíkban, és abban az esetben a rendszer lineáris egyenlőtlenségek - része a sík által határolt több sor, szükség ahhoz, hogy a rajzot.
A megoldás a rendszerek lineáris egyenlőtlenségek egy nagyszámú változót, csökkenti számos gazdasági kihívást jelent, különösen, egy lineáris programozási feladat. amely szükséges, hogy megtalálják a maximum vagy minimum egy függvény.
Nézzük először lineáris egyenlőtlenségek a gépen. Tekintsünk egy egyenlőtlenség két változó, és:
ahol - együtthatók a változók (egyes szám), - a konstans tag (a szám).
Egy egyenlőtlenség két ismeretlen, valamint az egyenlet van egy végtelen számú megoldást. A megoldás ezen egyenlőtlenség hívunk számpár, amelyek megfelelnek ennek az egyenlőtlenség. Geometriailag meghatározott megoldás a egyenlőtlenség van ábrázolva, mint egy fél-sík által határolt egyenes
akkor jelenik meg, a határvonal.
1. lépés: Készítse el a vonalak határoló megoldás halmaza lineáris egyenlőtlenség
Ehhez tudnunk kell, hogy bármely két pont a vonal. Találunk metszéspontjai a koordináta-tengely. Az ordináta a metszésponttól egy nullával egyenlő (1. ábra). A számszerű értékek a tengelyek ez a szám utal az 1. példának Nézzük ezt követően azonnal tereticheskogo kirándulás.
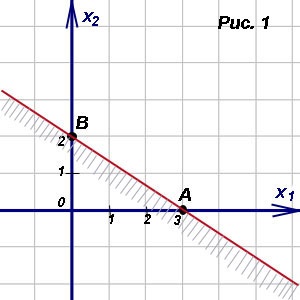
Abszcissza talál, mint a rendszer közvetlen egyenlet megoldását a tengelyen.
Megtaláljuk a metszéspontja: