A rendszer lineáris algebrai egyenletek
A rendszer lineáris algebrai egyenletek ismeretlen - egy olyan rendszer egyenletek formájában
Itt - ismeretlen kell meghatározni. Együtthatók rendszer „/> és annak szabad kifejezéseket feltételezzük, hogy ismert. Coefficient indexek” /> kijelölt rendszer számú egyenletek és ismeretlenek, ahol a költség tényező.
A rendszer homogénnek nevezzük. ha minden változatlan feltételek nulla, vagy - nem egyenletes.
A rendszer neve egy négyzet. ha a szám egyenletek száma megegyezik az ismeretlenek.
Megoldás a rendszer - egy sor olyan számok, hogy minden egyes helyettesítési helyett a rendszer felhívja az összes egyenletet figyelembe identitást.
A rendszer nevű együttes. ha van legalább egy megoldást, és következetlen. ha nincs megoldás. A közös rendszer egy vagy több megoldásokat.
Megoldások és együttműködési rendszer úgynevezett eltérő. Ha megsértik legalább az egyik egyenlet:
A közös rendszer neve biztos. ha van egy egyedülálló megoldás; ha van legalább két különböző megoldást, ez az úgynevezett határozatlan. Ha az egyenlet nagyobb, mint az ismeretlen, ez az úgynevezett túlhatározott.
mátrix formában
A lineáris egyenletrendszer lehet képviselve mátrix formában, mint
Egy példa a lineáris egyenletrendszer
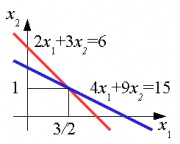
Grafikus oldatot egy lineáris egyenletrendszer
A rendszer két egyenlet két ismeretlennel adják
Ahhoz, hogy megtalálja az ismeretlen megoldandó tekintetében a felső egyenletet: x_2 „/>, majd helyettesíteni a kapott oldatot aljába egyenletet: x_2 \ right) + 9x_2 = 15.” /> A megoldás, „/>.
Ez a rendszer lehet vizuálisan képviseli a grafikonon formájában két sorban. A pont koordinátái 1) „/> egy megoldást.
módszerek oldatot
Közvetlen (vagy pontos) módszerek Lineáris rendszerek megoldások segítenek megoldást találni egy bizonyos számú lépést. A direkt módszerek közé tartozik a Gauss módszer. Gauss - Jordan Cramer módszerrel, egy mátrix módszer és söprés (a tridiagonális mátrix) módszerrel.
Iteratív módszerek alkalmazásán alapuló egy iteratív folyamat. Ez lehetővé teszi, hogy egy megoldást követő közel. Iteratív módszerek közé tartozik az eljárás, Jacobi (egyszerű iteráció), Gauss - Seidel relaxációs módszer és multigrid.