A normális eloszlás és tulajdonságai
Normális eloszlás görbe az úgynevezett normál vagy Gauss-görbe. Ez az eloszlás megfelel a jogszabályi előírásoknak, nyitott három tudós különböző időpontokban: Moivre 1733 Franciaország, a Gauss 1809-ben Németországban és Laplace 1812-ben Franciaországban.
ahol u - görbe magassága fölött közvetlenül bármilyen előre meghatározott értéket x a gyakorisági eloszlását gráf;
e - az alapja a rendszer természetes alapú logaritmus = 2,718.
AIS - számok, amelyek meghatározzák a görbe pozícióját a valós tengelyen és szabályozzák annak terjedelmét.
Ütemezése normális eloszlás az úgynevezett szimmetrikus haranggörbe. Változtatásával értékeit és s, tudjuk mozgatni az adott normális görbe a valós tengelyen lefelé és felfelé megváltoztatni a méretét.
A mennyiség a megfelel az átlagos gyakorisági eloszlását nagy minta (elvárás); s - szórása ezen eloszlás. Így a paraméter a (elvárás) jellemzi a pozíció és a paraméter s 2 (diszperzió) - forma egy normális görbe.
Normál jog valószínűségi változó paraméterekkel a = 0, s = 1 2. azaz N (0, 1) nevezzük egy szabványos vagy normalizált. és a megfelelő normál görbe - a standard vagy normalizált. Által határolt területen ez a görbe = 1.
Mert bármilyen kombinációja normál görbe egység végre meglehetősen egyszerű átalakulás kezdeti eloszlása kivonva az átlagos értéket minden egyes pontok Xi és elosztjuk s.
A normális eloszlás jellemzi szélsőértékek található benne ritkák, és az értékek az átlag közeli - elég gyakran. A normális eloszlás hívják, mert nagyon gyakori a természetes - a tudományos kutatás és úgy tűnt, „normális” bármilyen tömeges véletlen megjelenése egy attribútum.
Normál görbe mindig szimmetrikusak a. A terület között a görbe és az x tengely egyenlő 1.
Tulajdonságait normál elméleti eloszlás
1) módban, a medián és a számtani középértéket azonos vagy hasonló értékek nagyságrendű;
2) paraméterek a ferdeség és csúcsossága nulla, AS = 0, és Es = 0.
3) Végzett tipikusan három Sigma.
Gyakori, hogy az összes ilyen görbe, akár normális eloszlás kb:
1. 68% a görbe alatti terület belül fekszik az egyik ok az átlag bármelyik irányban (azaz ± 1 s);
2. 95% a görbe alatti terület belül van két átlagos s mindkét irányba (azaz ± 2s);
3. 99,7% a görbe alatti terület közötti tartományban az átlagos három s mindkét irányba (azaz ± 3s).
Három szigma szabály a nyelv a valószínűségszámítás:
Annak a valószínűsége, hogy a több X tartományba esik a | X-mê
A) Ha szimmetrikus eloszlás jellemző mindkét oldalán A szelektív táptalaj defer egyenlő távolság s, akkor magában 2/3 megfigyelések (normális eloszlás, 68% -ában).
B) A intervallumban X = [HSR ± 2s] 95% -ában.
B) A intervallumban X = [HSR ± 3s] 99% -ában (a normális eloszlás a 99,73% -ában).
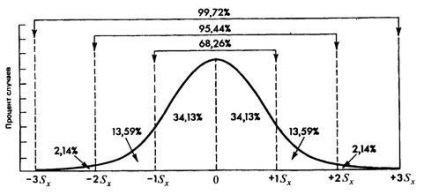
Ábra. 3. ütemezése standard normális eloszlás jellemző.
Amikor homogén nyert mintában a téma, hogy egy előre meghatározott módon a normális eloszlás, a számtani ezen eredmények középértékét HSR és a standard eltérést s eredménye meghatározzuk egy mintában határ statisztikai norma [HSR ± s].
Ábra. 4. A grafikon normális eloszlását jellemző
Eloszlásának normalitását a kapott változó lehet ellenőrizni, hogy kiszámítjuk a kurtózis és aszimmetria-indexek és összehasonlítjuk azokat a kritikus értékek (kritérium NA Plohinskogo vagy Pustylnik EI). Betartásának ellenőrzését a tapasztalati eloszlása normális, valósítható kritérium szerint # 967; 2 -Pirsona.
Criterion NA Plohinskogo
Számított hibahatáron ferdeség és csúcsossága:
ahol n a minta térfogata
Ha a ferdeség és csúcsossága paraméterek haladja meg a három vagy több alkalommal, abszolút értékben a hibát reprezentativitás, az empirikus eloszlás eltér a normális.
Criterion EI Pustylnik
Kiszámítjuk a kritikus értékei ferdeség és csúcsossága
ahol n a minta térfogata
Ha tapasztalati értékek ferdeség és csúcsossága többet, mint a kritikus értékek> ACR és Es> Ecr. Az empirikus eloszlás eltér a normális.