A kapcsolat a csoport és a fázis sebességek
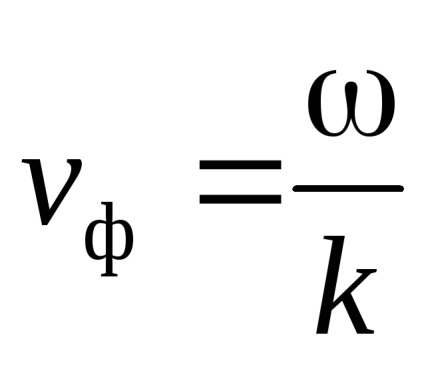

A nem-diszperzív közeg
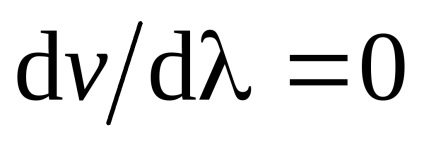
A koncepció a csoport sebesség nagyon fontos, mert úgy tűnik, pontosan mérve radar hatókörén űreszközökben rendszerek stb A relativitáselmélet bebizonyosodik, hogy a csoport skorostu
5. interferencia hullámok
Ez az úgynevezett koherens interferencia időben és térben áramlik több hullám folyamatok, amelyet úgy kapunk, hozzáadjuk a nyereség vagy a csillapítás a kapott hullám.
Összefüggő beavatkozás fogalmának összhangját. Waves nevű koherens, ha a fáziskülönbség minden pontján térben tartjuk állandó.
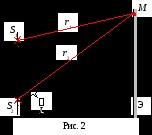
Legyen az egyenlet a két koherens gömb alakú hullámok egymásra helyezett, kapnak formájában
S1 =
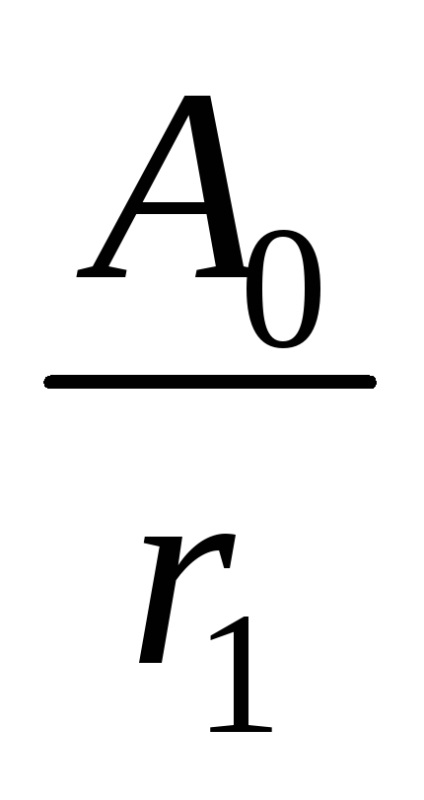
S2 =
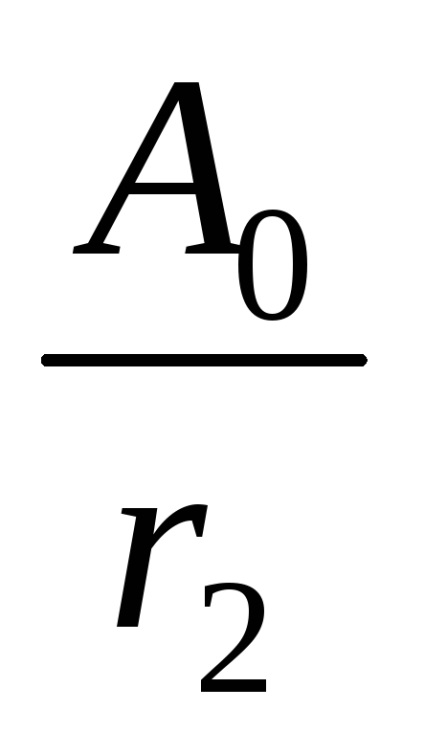
A amplitúdója a kapott hullám
Mivel koherens források különbség a kezdeti fázisok (1 2) = const, az eredmény a hozzáadásával oszcilláció különbségétől függ hullám löket
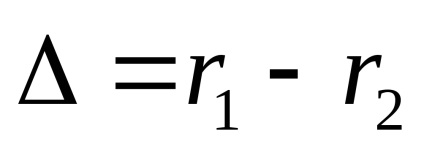
Interferencia maximális állapot
az amplitúdó a re-Dhul tiruyuschego ingadozások
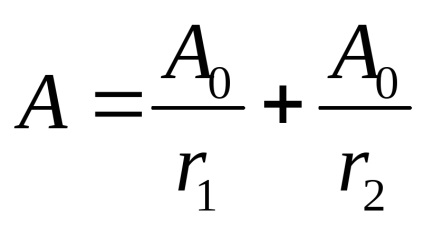
Feltétel interferencia minimális
az amplitúdó a kapott oszcilláció
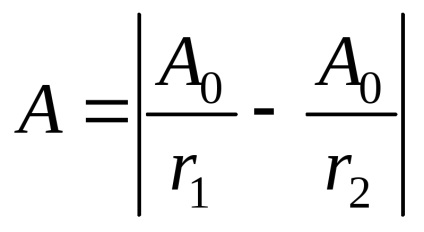
mporyadok interferencia maximális vagy minimális.
állóhullámok
Állóhullámok egy adott esetben az interferencia és a képződnek szuperponáljuk két utazó hullámok szaporító ellentétes irányban azonos frekvenciájú és amplitúdójú.
Hozzáadása ezeket az egyenleteket, és figyelembe véve, hogy k = 2 / , megkapjuk



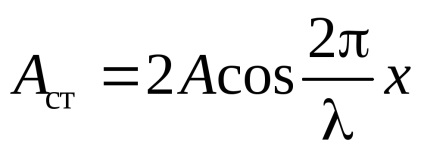
A pontok, amelyeknél a rezgési amplitúdója maximális (Ast = 2A) nazyvayutsyapuchnostyami állóhullám, és a pont, ahol a rezgés amplitúdója nulla (Ast = 0) uzlami állóhullám.
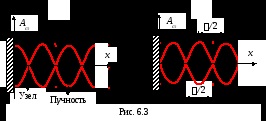
koordináták amplitúdópontok
A koordináták a csomópontok
A formáció állóhullámok figyelhető meg a beavatkozást az utazóközönségnek és a visszavert hullámok. Mi történik a határon, vagy amplitúdópont uzel reflexió arányától függ közepes sűrűségű. Ha a közeg, amelyben a reflexió kevésbé fordul elő sűrű helyett a visszaverődés kapunk amplitúdópont ha sűrűbb - csomópont. Ha az energia nem kerül át az állóhullám.
Szaporítása longitudinális hullám impulzust a rugalmas rudat.
A jellemző mechanikai hullámok, hogy azok elosztott egy kézzelfogható adathordozón (szilárd, folyékony vagy gáz-halmazállapotú). Vannak olyan hullámokat terjeszteni képes vákuum (például, fényhullámok). A mechanikus hullámok feltétlenül kell egy olyan környezet, amely képes tárolni mozgási és helyzeti energia. Következésképpen, a közeg inertnek kell lennie, és rendelkeznie elasztikus tulajdonságait. A valós környezetben, ezek a tulajdonságok szét az egész kötetet. Például, bármilyen kis eleme merev test tömege és rugalmasságát. A legegyszerűbb egydimenziós modell egy merev test lehet ábrázolni, mint egy sor golyó és rugó (ábra. 2.6.3).
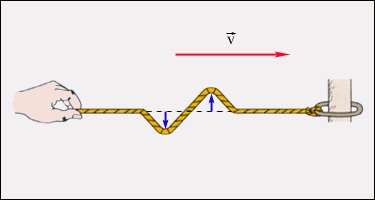
Egy egyszerű egydimenziós modell egy merev test.
Ebben a modellben, inert és rugalmas tulajdonságai vannak osztva. A gyöngyök van tömege m. és rugók - merevség k. Egy ilyen egyszerű modell leírására terjedésének hosszirányú és keresztirányú hullámok szilárd. A longitudinális hullámok golyó tapasztalható elmozdulás a lánc mentén, és a rugók vannak nyújtva vagy sűrített. Ez a deformáció nevezzük deformációját préseléssel vagy stretching (lásd. §1.12). Folyadék vagy gáz az ilyen típusú kíséri deformáció a tömítés vagy vákuum.
Longitudinális mechanikai hullámok terjednek bármely médiában - szilárd, folyékony és gáz halmazállapotú.
Ha a váltás a merőleges irányban a lánc, van egy nyíró deformációt a egydimenziós modell egy szilárd, egy vagy több golyó. Deformált során ez az elmozdulás a tavaszi hajlamos visszatérni az elmozdult helyzetben egyensúlyi részecskék. Ebben az esetben a következő elfogulatlan részecskék jár rugalmas erő igyekszik eltéríteni őket az egyensúlyi pozíciókat. Ennek eredményeként, a lánc fut végig a keresztirányú hullám.
A folyadékok és gázok rugalmas nyírási deformáció nem fordul elő. Ha az egyik réteg egy folyadék kiszorítja egy bizonyos távolságot képest szomszédos réteg, nincsenek tangenciális erők közötti határfelületen a rétegek nem jelenik meg. A ható erők a felület között egy folyadék és egy szilárd, és az erők közötti szomszédos rétegek a folyadék mindig mentén irányul a szokásos a határ - ez nyomóerő. Ugyanez vonatkozik a gáz-halmazállapotú közeg. Következésképpen, a keresztirányú hullámok nem létezhet folyékony vagy gáz-halmazállapotú környezetben.
Jelentős érdeklődés a gyakorlatban egyszerű harmonikus vagy szinuszos hullámok. Jellemzőjük a rezgések amplitudoyA részecskék chastotoyf és l a hullámhossz. Szinuszos hullámok terjednek a homogén közegben állandó sebességgel υ.
Az elmozdulás y (x. T) a közeg részecskéi az egyensúlyi helyzetből egy szinuszhullám függ X koordináta a OX tengelyen. amely mentén a hullám terjed, és a t idő a törvény szerint:
ahol - nazyvaemoevolnovoe számát. ω = 2pf - körkörös frekvencia.
Ábra. 2.6.4 mutatja „pillanatfelvételek” a keresztirányú hullám két időpontban: t és t + dt. Alatt At hullám tengelye mentén OX olyan távolságra υΔt. Hullámok, minden pont, ami mozog ugyanilyen sebességű, általában az úgynevezett futó (szemben álló hullámok cm. Alább).
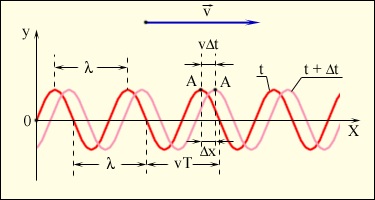
„Snapshot” egy utazó szinuszjellel időben t és t + At.
Hullámhossz λ nevezik a távolságot két szomszédos pont a tengely OX. oszcilláló ugyanabban fázisban. Egyenlő távolság a hullámhossz λ, a hullám tartományok időszakban T, tehát, λ = υT. ahol υ - hullám terjedési sebessége.
Bármilyen kiválasztott pontra a grafikonon a hullám folyamat (például, hogy az A pont ábrán 2.6.4.) Az expressziós ωt - KX nem változik a mérete. Az idő múlása t és változások a koordináta x a pont. Egy időintervallum után At pont mozog az OX tengely bizonyos távolságra x = υΔt. ezért:
Modell. Longitudinális és transzverzális hullámok.
Ha a mechanikus hullám szaporítóanyag a közegben találkozik az útjába akadályt, akkor drasztikusan megváltoztathatja a magatartás természetét. Például, a hullám részben visszaverődik a felület közötti két közeg a különböző mechanikai tulajdonságú, és részlegesen behatol a második közeg. Hullám mentén haladva egy string vagy gumiszalagot visszaverődik a fixen szerelt végét; így van egy hullám utazik az ellenkező irányba. A karakterlánc van rögzítve, mindkét végén vannak olyan komplex rezgések, amelyek úgy tekinthetők, mint egy szuperpozíció (szuperpozíciója) a két hullám utazik ellentétes irányban, és mennek keresztül visszaverődések és a többszörös visszaverődés a végein. A rezgések a sztring rögzített mindkét végén, ami a hangok minden húros hangszerek. Nagyon hasonló a jelenség, amikor a szél hangját eszközök, köztük a orgonasípokat.
Ha a hullámok mentén haladva a húr ellentétes irányban, szinuszos alakú, alkothatnak egy állóhullám bizonyos feltételek mellett.
Legyen a húr l hosszúságú rögzített úgy, hogy az egyik végén található az x = 0, és a másik - az x = l (ábra 2.6.5.). A string létrehozott feszültségi T.
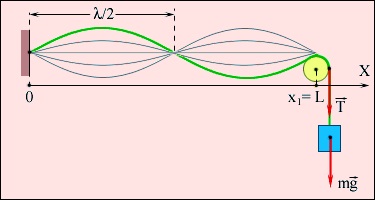
A formáció állóhullám egy húr fix mindkét végén.
A húr egyidejű alkalmazása két hullám ellentétes irányban ugyanolyan gyakorisággal:
Azon a ponton, x = 0 (az egyik a rögzített végei a húr) a beeső hullám y1 a reflexiós hullám generál y2. Upon tükröződés a rögzítetten szerelt végén a visszavert hullám ki fázisban a beeső. Szerint a szuperpozíció elve
Ez egy állóhullám. Az állóhullám, vannak fix pontok az úgynevezett csomópontok. Félúton a csomópontok pontokat, hogy változik a maximális amplitúdója. Ezek a pontok az úgynevezett amplitúdópontok.
Két fix végén a húr kell csomópontokat. A fenti képlet kielégíti ezt a feltételt a bal végén (x = 0). Teljesíti ezt a feltételt, és a jobb végén (X = l), az szükséges, hogy KL = n π, ahol n - bármilyen egész szám. Ez azt jelenti, hogy az állóhullám jelentkezik a húr nem mindig, de csak abban az esetben, ha az l hosszúságú sztring egyenlő egész számú félhullámából:
Egy sor értékek hullámhosszának megfelelő λn sor lehetséges frekvenciák fn:
ahol - a terjedési sebessége transzverzális hullámok a húr. Mind a társult frekvenciák típusú karakterlánc rezgés nazyvaetsyanormalnoy divat. A legalacsonyabb frekvencia a alapfrekvencia f1. minden más (f2. f3. ...) harmonikusok. Ábra. 2.6.5 szemlélteti a szokásos módon az n = 2.
Az állóhullám nem energia áramlását. Rezgési energiát tartalmaz, amely részben a húr két szomszédos csomópont, nem szállítják más részein a húr. Minden ilyen szegmens egy periodikus (kétszer időszakonként T) átalakítása kinetikus energia átalakul potenciális energia és fordítva, mint a hagyományos oszcilláló rendszer. De ellentétben a terhelést a tavaszi vagy az inga, amelyben csak egyetlen természetes frekvenciája a húr végtelen számú természetes (rezonáns) chastotfn. Ábra. 2.6.6 ábrázolják többféle állóhullámok egy húr fix mindkét végén.
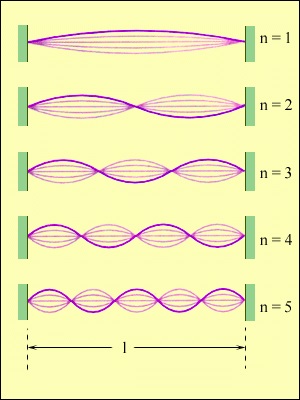
Az első öt normál módban rezgések egy sor fix mindkét végén.
Összhangban a szuperpozíció elve állóhullámok a különböző típusú (azaz. E. különböző értékei n) lehet egyidejűleg jelen a karakterlánc rezgések.