9. osztályba
Feltérképezése a gépet magára.
Minden fogalmakat, hogy bevezetésre kerül az általunk ebben a részben, sőt, már korábban tanulmányozták, azzal a különbséggel, hogy most fogjuk be őket általánosságban.
Tengelyszimmetrikus - egyfajta szimmetria, amelyben minden egyes pontja a sík, például az M pont (1. ábra) egy bizonyos törvény van rendelve egy másik pontja ugyanabban a síkban.
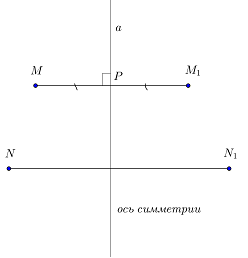
A törvény, amely szerint ez a levelezés folyik, az alábbiak szerint:
Től az M pont a merőleges vonalat kapunk, és a P pont, a metszéspont a merőleges a tengelyre. Késleltetett részes RM1 = PM, és a lényeg az M1. Így, bármely pontja M a sík van rendelve egy egyedi pont M1 síkon, ahol:
1. MR ^ a, p - a metszéspont
2. RM1 = RM. ahonnan megkapjuk a pont M1
Ugyanakkor, mi támaszkodott egy jól ismert geometriai tény: a M pont lehet elvégezni csak egy vonal merőleges egy adott vonal.
A fordított művelet: ha a tengelyirányú szimmetria az M pont van rendelve egy pontot az M1, az a pont M1 megfelel egy M pontban
Ugyanez a folyamat lehet végezni, és a megfelelő pár N pontokat N1 és ugyanabban a síkban (ábra. 1), és ha tudjuk, hogy az a pont N1 amely hozzá van rendelve egy pont n, akkor tudjuk, hogy a pont maga és N. Tehát, minden egyes pontja a sík társul egy másik pont a gépet. És minden pont a síkban van a megfelelő pontot.
Tengelyszimmetriát egy speciális esete az ún kijelző nasebya síkon.
Egy másik speciális eset a kijelző sík önmagára központi szimmetria.
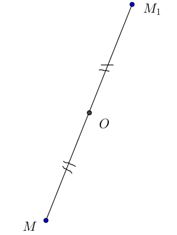
M sík pont mozog, hogy egy pont M1 más síkon a következő módon (2. ábra) .:
1. egyenes MO
2. ez a vonal megy tovább és elhalasztják részes OM1 = OM, megkapjuk a pont M1
M1 van rendelve egy pont M.
Mindkét bemutatott példák a térképek a következő tulajdonságot:
ha egy hosszú MN szakasz, akkor beköltözik a szegmens M1N1 azonos hosszúságú, azaz. e. a távolság bármely két pont között tárolják.
A következő a gépet, amelyen minden távolságra megmaradnak nazyvaetsyadvizheniem,
t. e. „sík távolodik és mentett.” Mozgását egy pár, mi tekinthető a kettő, azaz az axiális szimmetria és a központi szimmetria. Most megmutatjuk, hogy minden egyes ilyen szimmetriák mozgás. Meg kell bizonyítani, hogy a távolságok tárolják.
Ennek bizonyítására tengelyszimmetriát.
Ily módon, amikor a leképezés M M1 →, N → N1, ahol a PM = PM1, NQ = QN1 (ábra. 3)
Be kell bizonyítanunk, hogy MN = M1N1.
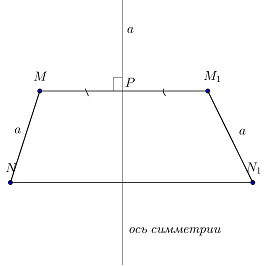
Forma a rajz (ábra. 4).
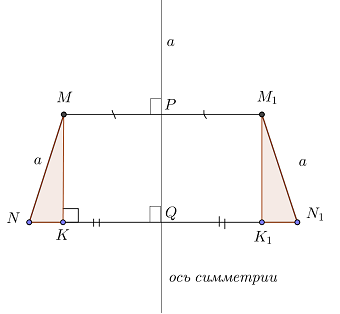
Hogy extra építésű, épült arra a pontra, hogy az MC ^ NN1,
Addigra a ponton jelenik meg azon a ponton, K1.
Megmutatjuk, az egyenlő derékszögű háromszöget és MNK M1N1K1. Ezekben háromszögek hossza érdekes számunkra, az átfogója, akkor bizonyítania kell, hogy a másik két oldala van.
MK = M1K1 két merőleges a párhuzamos vonalak.
Ábrából. A 4. ábra mutatja, hogy az NK = NQ - KQ és N1K1 = N1Q - K1Q. Ezekből az egyenletekből és állapotok, amelyek az N pont jelenik meg a N1 pont azt jelenti, hogy az NK = N1K1.
Azaz, két háromszög egyenlő Catete, és így egyenlő és a átfogója, amely MN = M1N1, szükség szerint.
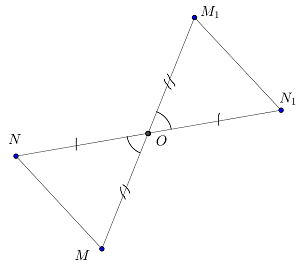
Mi most azt mutatják, hogy a központi szimmetria is egy mozgalom. Ábra kiegészítése. 2 pont N, és a pont N1, amelyben az első pont jelenik meg a közepén szimmetria (ábra. 5).
Ehhez össze egy szegmens, és a folytatás - részes ON1, kap egy pontot az N1. Így ON1 = ON. Be kell bizonyítanunk, hogy MN = M1N1
két oldalán és a köztük lévő szög (ÐMON = ÐM1ON1 függőleges, és a megfelelő oldalán a háromszögek miatt a központi szimmetria törvények).
Azaz, bármilyen távolságban központi szimmetria megmarad. Így a mozgás a központi szimmetria.
Tehát, megnéztük a kijelző repülőgép-ra is. Tekinthető két példa a képsík: axiális szimmetria és a központi szimmetria. És észre egy fontos körülmény, hogy minden távolságok ezekhez az átalakításokhoz tárolja. Azok átalakítások a gép saját magára, hogy megőrizze az összes távolságot nevezzük mozgását. Bebizonyítottuk, hogy az axiális szimmetria mozgás és a mozgás központi szimmetria.