7. feladat érintő a grafikont
B9, van egy osztály a problémák, melyben kap egy ütemezés funkció. Annyit lehet tudni - függvénye az egyenletet és az érintő. És ma megtanuljuk megoldani egy ilyen problémát.
Mi megoldani valós példa
Tehát az első feladat:
Közvetlen \ [y ~ = 16x-38 \] az érintő a függvény grafikonját:
Keresse abszcissza az érintési pont.
Először is, hadd minden emlékszik, hogy érinti a függvény grafikonját. Tehát van egy ütemtervet, valamint közvetlen, amely kapcsolódik ehhez a grafikonon, azaz metszi a diagram csak egy ponton, a szög keresztezi a tengelye $ Ox $, pontosabban a tangense ez a szög értékével egyenlő a származtatott ezen a ponton ..:
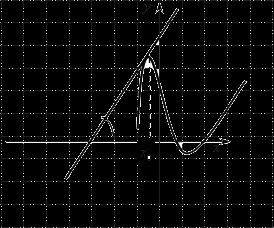
Most lefordítani a hivatalos meghatározás az ember által olvasható nyelvet. Egyrészt azért, mert a mi egyenes a következő egyenlet adja, egy érintőleges, ezek az egyenletek szükségszerűen van egy közös pont, hogy van. E., Van egy közös megoldást. Ezért is érezze, hogy a jobb oldalon, azaz a. E.:
Másrészt, mert ez egy érintőleges a grafikon, hanem egy tetszőleges keresztmetszetű, akkor kérheti, hogy tartalmazza nemcsak a funkciók maguk, hanem ezek származékai, azaz a. E.:
Térjünk az első kifejezés:
Itt van az első design. Ez az egyenlet a harmadik fokozatot. Hogy oldja meg, akkor próbálja elbontására polinom a tényezőket, és valóban, miután bizonyos átalakítások és néhány sornyi számítások kap egy pár jelöltet a választ. Azonban ne feledjük, hogy ez egy egyszerű feladat az EGE a matematika, azzal a feladattal, B. rész Ezért kell megoldani sokkal könnyebb, anélkül terjeszkedést. És emiatt már megkapták a második egyenletben. Már hasonlítható származékok, és most nézzük őket számolni:
Kaptunk másodfokú egyenlet. Ez az identitás könnyen megoldható, és a diszkrimináns képletek és Wyeth. Nézzük megoldani a következő képlet szerint Térség:
\ [\ Bal (-3 \ right) \ bal (+1 \ right) = 0 \]
Tehát van két gyökér, a két jelölt a választ, t. E. Azok abszcisszák amelynél a származékot mi érinti a függvény grafikonját egyenlő a származék. Most vissza az eredeti tervezési és arra gondolunk, hogy amellett, hogy a funkciók maguk származékok is kell egyenlő, azaz. E. Mi kapott „X” választani azokat, amelyek megfelelnek az egyenletet. Nézzük helyettesítő \ [= 3 \]:
Nyilvánvaló, hogy \ [= 3 \] gyökere mindkét kifejezés - és a mi eredeti és származtatott. Ennél a végén megoldás, de nézzük megbízhatóság és behelyettesítjük \ [= - 1 \]:
\ [- 1-3 \ cdot 1-9 \ cdot \ bal (-1 \ jobb) + 27 = 0 \]
Egyértelmű, hogy ez a kifejezés nem az egyenlőséget. Következésképpen \ [= - 1 \] nem gyöke identitásunkat. Arra a következtetésre jutottunk, hogy egyetlen gyökér, kielégítve minden követelmények \ [= 3 \]. Ez a válasz a problémára. Találtunk abszcisszájának az érintkezési pont a menetrend.
Főbb pontok
Összefoglalva, hadd ismét megy át a fő lépéseket megoldásokat.
Az első helyen, ami azt jelenti, hogy a vonal is érintő függvény grafikonját? Ez azt jelenti, hogy a közvetlen és $ f \ left (x \ right) $ van egy közös megoldás. Ezért tudjuk egyenlőségjelet tesznek a $ y $ a kifejezéseket. Kapunk az első identitását.
Azonban a megtérése után, megkapjuk az egyenlet a harmadik fokozat, és mint ilyen, a struktúra általában megoldott elég nehéz, és van néhány gyökér, mi rögzíti a kisegítő egyenlet, emlékezve arra, hogy beszélünk érintő a függvény grafikonját, azaz a. E. mint a valódi $ f \ left (x \ right) $ egyenlőnek kell lennie egymással, és ezek származékai. Ebben az esetben, a származékos ügyletek tekinthetők egyszerű. Összesen kapunk egy egyszerű másodfokú egyenlet, amely aztán könnyen megoldható, és kiderül két gyökér.
A kérdés az, hogy ezek közül melyik gyökerek a helyes válasz? Ahhoz, hogy megtalálja a helyes választ, nagyon mindegyik szám helyettesíti a mi egyenletben, megvan az elején. Itt jutunk, hogy az egyik gyökerek vagyunk teljesen elégedettek, és a második gyökér - nem, hogy van, ez határozottan nem megoldás ...
Abból a szempontból a geometria, a következő történik. Tegyük fel, hogy van itt egy ilyen funkció:
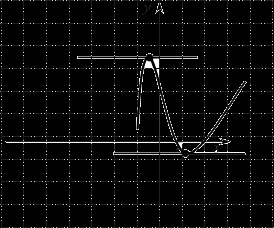
Van egy maximális pontot és a minimális pontot. Mindkét esetben a derivált nulla, ezért húzott érintő keresztül minden ilyen pont is van egy származéka értéke 0, azaz a. E. vízszintes. Azonban, mint láttuk, van egy érintőleges függvény grafikonját. Ha az érintő átmegy a felső, nem lesz képes átlépni a görbe az alacsonyabb értéket. Épp ellenkezőleg, ha figyelembe vesszük az érintő a legalacsonyabb ponton, akkor nem lesz képes átlépni a görbe a felső szintre. Ez magyarázza, hogy bár a származék egy származéka érintő két ponton, a végén a mi egyenletben találkozunk csak az egyiket.
- Ingyenes Felkészülés a vizsgára 7 egyszerű, de nagyon hasznos tanulságokat + házi feladat
