Függőleges érintőleges grafikont - studopediya
Majd azt mondjuk, hogy az a pont függvény grafikonját van egy függőleges érintője,
a következő egyenlet adja (1b)
1. példa 1. Legyen a grafikonon funkciókat kapnak két pontot. Keressük a következő egyenletet:
1) szelő pontokon átmenő
2) Az egyenletek az érintő vonalak a grafikon lefolytatott
Határozat. 1) Határozza meg a lejtőn a szelő ponton áthaladó
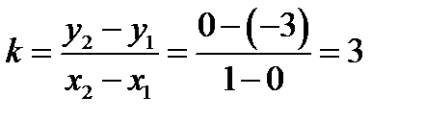
;
Használata tangens szögek között meghatározott grafikonok funkciók a pont a kereszteződés.
Meghatározás 1.4. Közötti szög a grafikonok a funkciók a metszéspontja közötti szög a tangens vonalak ezen a ponton ábra. 2. Ezt a szöget a következő képlettel
hegyesszög által meghatározott (1,4) közötti
2. ábra. érintők.
Megjegyzés. Meghatározása a származék sokkal kényelmesebb rögzíteni és használni segítségével lépésekben.
Definíció 1.5. Lépésekben nevű argumentum különbség, és jelöljük. = A különbség az úgynevezett növekmény a függvény.
Így, a meghatározása a származék lehet újraírni az
Megjegyzés. Származékok lehet rögzíteni a következő szimbólumokkal
1.2 példa. A meghatározás (1.5), azt látjuk, a származékos funkciók egy ponton.
Határozat. Használata a meghatározása a származék (4,5), kiszámíthatjuk a növekmény a függvény a ponton. Aztán.
A meghatározás (1.5), azt látjuk, a függvény deriváltját.
A definíció szerint van
A fizikai értelmében a származék. Hagyja, hogy a megtett út egy pont mentén mozgó egyenes, változik az idővel a törvény szerint. akkor az átlagos sebesség a ideig úgy definiáljuk, mint;
Pillanatnyi sebesség, az idő (definíció szerint), az átlagos sebesség határt;